[科普中国]-符号距离函数

符号距离函数（sign distance function），简称SDF，又可以称为定向距离函数（oriented distance function），在空间中的一个有限区域上确定一个点到区域边界的距离并同时对距离的符号进行定义：点在区域边界内部为正，外部为负，位于边界上时为0。

定义如果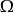 是一个度量空间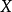的子集，度量 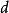，则符号距离函数 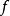由下式定义1

1）如果 ， ；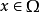

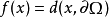2）如果 ， 。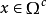

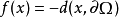其中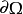， 表示边界的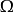 。对于任何 ，

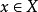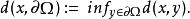其中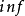 表示下确界。

在欧几里得空间属性如果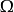 是具有分段平滑边界的欧几里德空间 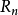一个子集，那么带符号的距离函数几乎在任何地方都是可微的，并且它的梯度满足方程

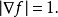
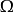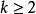如果 的边界对于 是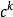 ，那么在充分接近 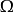边界的点上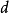， 是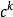 。尤其在边界 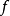满足

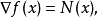其中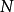 是内部法向矢量场。有符号距离函数因此是法向量场的可微分延伸。特别地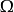， 边界上的带符号距离函数的Hessian给出了Weingarten映射。进一步，如果是一个足够接近Ω边界的区域，那么 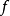是两次连续可微分的，那么就存在一个明确的公式，该公式涉及Weingarten映射 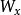，用于根据有符号距离函数改变变量的雅可比矩阵和最近的边界点。具体地，如果 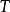是距离内的点的集合 的边界的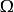 （即管状邻域半径的 ），并 是上一个绝对积函数Γ，然后

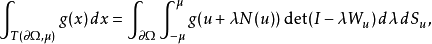其中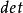 表示行列式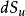， 表示表面积分2。

应用例如，在计算机视觉中使用签名的距离函数。如使用了一种方法（由Valve Corporation开发），使用GPU加速来渲染大尺寸（或者高DPI）的平滑字体。Valve的方法计算了光栅空间中的有符号距离场，以避免解决（连续）向量空间中问题的计算复杂性。最近已经提出了分段逼近解决方案（例如，近似具有弧形样条的Bézier），但即使如此，计算对于实时渲染而言可能太慢，并且必须通过基于网格的离散化技术来近似（并从计算中剔除）到距离太远的点的距离。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所