[科普中国]-交替式图灵机

图灵机在理论上能够模拟现代数字计算机的一切运算， 可视为现代数字计算机的数学模型，是一种抽象的计算模型。交替式图灵机（Alternating Turing Machine，ATM）是计算复杂度理论中定义的一种非确定型图灵机（NTM）。与一般非确定型图灵机不同，交替式图灵机将接受语言的规则一般化到NP和反NP。交替式图灵机的概念由Chandra和Stockmeye于1976年提出。

定义直观描述NP的定义中使用了语言的存在形式，亦即如果存在一个选择都能够使得图灵机达到接受状态，那么整个语言就能够被接受。与此对应，反NP的定义中使用了语言的全称形式，亦即整个语言被接受，当且仅当每一个选择都达到一个接受状态。结合这两个定义，可以给出一个语言被交替式图灵机接受的定义。

对一台交替式图灵机而言，状态集被划分为两部分：存在状态（existential state）和全称状态（universal state）。存在状态的接受条件为如果该状态存在一种转移序列到达接受状态，而全称状态的接受条件为对该状态而言，任何一种转移序列都能够到达接受状态。（因而，一个不包含任何转移的全称状态无条件接受，而一个不包含任何转移的存在状态无条件拒绝。）交互式图灵机接受此语言，当且仅当初始状态得到接受。

形式化描述 形式地，一台（单带）交替式图灵机是一个5元组，其中：

是一个有限大小的状态集；

是一个有限大小的字母表；

被称为转移函数（ 代表带头左移， }代表带头右移）；图灵机状态可以转移到状态

是初始状态，开始时控制就在这一状态上；

定义每个状态的类型（接受状态或拒绝状态），其中 代表全称状态， 代表存在状态。，其中表示读写头是向左移还是向右移, - 表示不移动，不同状态可以随着字符转换。

如果 的格局在状态 中，且 ，那么，格局为接受格局。如果格局满足 ，那么，格局为拒绝格局。对于格局满足 ，该格局接受当且仅当所有一步之内能够到达的格局是接受格局。反之，如果这些格局中存在一个格局拒绝，那么拒绝。对于格局满足 ，该格局接受当且仅当存在一个一步之内能够到达的格局是接受格局。反之，如果所有一步之内可达的格局拒绝，那么拒绝。 接受输入串 ，如果的初始格局（即 的状态为 ，带头在带的最左端，带中包含 ）被接受。否则， 拒绝 。

k次交替图灵机k次交替图灵机是一种将存在状态和全称状态互相转移次数限定在 次的交替式图灵机。亦即，定义状态集 ，其中，状态集 为存在状态，状态集 为全称状态（或者相反）。并且，不存在从 到 的状态转移满足 。例如，考虑以下电路最小化问题：给定一个能够计算布尔函数 的电路 和一个整数 ，确定是否存在一个最多包含 个门的电路 可以计算 。一台2次交替图灵机从一个存在状态出发可以在多项式时间内解决这个问题（在存在状态通过猜测电路 的 个门，此后进入全称状态，猜测输入并检查输出是否和 相同）。一台从存在状态（或者全称状态）出发的次交替图灵机可以在多项式时间内解决 （或者 ）的问题。

资源上界在利用上面的定义确定一台交替式图灵机是否接受或拒绝某一格局时，并不需要检查当前格局可以到达的所有格局。具体来说，对于存在格局，如果某一将来格局被接受即可标记为接受。对全称格局，如果某一将来格局被拒绝，则可被标记为拒绝。对于运行时间，规定一台ATM在 时间内判定一个形式语言，如果对于任意长度为 的输入，通过 步检查（必要的）格局即可接受或拒绝初始格局。对于运行空间，规定一台ATM在 空间内判定一个形式语言，如果至多修改图灵机带上从左端起 位即可完成对必要格局的检查。

示例也许交替式图灵机解决的最简单的问题是量词布尔公式问题。这一问题是布尔可满足性问题的扩充，即每个变量可以被一个全称量词或存在量词所约束。交替式图灵机依照约束的次序对每一个存在量词寻找一个可能的赋值，对每一个全称量词寻找所有的赋值。在对所有约束变量确定值之后，交替式图灵机根据剩余的布尔公式确定接受还是拒绝。因此，接受一个存在量词意味着存在一个赋值，使得赋值后的量词布尔公式可满足。类似地，接受一个全称量词意味着对任何一个赋值，赋值后的量词布尔公式可满足。在ATM中，解决量词布尔公式问题需要 时间和 空间。布尔可满足性问题可被视为量词布尔公式问题将所有变量约束为存在量词的特例。从而普通的非确定型图灵机可以有效地解决这一问题。

图灵机图灵机由图灵（Alan Turing）于 1936 年提出，当时的主要目的是为了理解计算问题的边界，即什么是可计算的。后来发现它是一种精确的计算机模型，可以模拟现实计算机的所有计算行为1。一切“可计算”函数都等价于图灵机可计算函数，而图灵机可计算函数类又等价于一般递归函数类。图灵机能表示算法、程序和符号行的变换，因而可作为电子计算器的数学模型，也可用作控制算法的数学模型，在形式语言理论中还可用来研究短语结构语言。非确定型图灵机和确定型图灵机的不同之处在于，在计算的每一时刻，根据当前状态和读写头所读的符号，机器存在多种状态转移方案，机器将任意地选择其中一种方案继续运作，直到最后停机为止。具体而言，其状态转移函数为

其中 是状态集合（包含初始状态、接受状态、拒绝状态和终止状态）， 是带字母表， 分别表示读写头向左和向右移动；符号 表示集合 的幂集，即

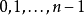开始的时候将输入符号串从左到右依此填在纸带的第号格子，他格子保持空白。非确定型图灵机 在输入串 上的计算过程可以表示为一棵树，不同的分支对应着每一步计算的不同的可能性。只要有任意一个分支进入接受状态，则称 接受 ；只要有任意一个分支进入拒绝状态，则称 拒绝 ；某些分支可能永远无法停机，但只要有一个分支可以进入接受或拒绝状态，我们就说 在输入 上可停机。注意，我们规定必须 是无矛盾的，即它不能有某个分支接受 而同时另一个分支拒绝 ，这样有矛盾的非确定型图灵机是不合法的。非确定型图灵机在计算能力上并没有因为加上了非确定性的状态转移而有所增强。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学