[科普中国]-波浪感生弯矩

波浪感生弯矩即船舶在波浪中运动时，相对于其在静水状态中所增加的弯矩。包括由于船舶水下体积形状变化、史密斯效应、惯性力及阻尼力等产生的各种成分。

详细描述随机海浪中船舶的波浪感生弯矩是正态狭带随机过程，其幅值服从雷利分布。可通过切片理论计算或规则波中模型试验给出纵向波浪生弯矩幅值的频率响应函数，并用谱分析法预报它的统计值1。波浪感生弯矩与由颤振、弹振等动载荷产生的附加弯矩(也称动弯矩)之和常称波浪弯矩。附加弯矩在某些情况下是不可忽略的。波浪弯矩与静水弯矩之和就是船舶的总纵弯矩。

波浪感生弯矩极值n次独立观测中可期望出现一次波浪感生弯矩的最大值。弯矩极值是一个随机变量，它的概率密度函数不同于波浪感生弯矩，可按序列统计学从波浪感生弯矩的概率密度函数及超越概率分布函数求得它的相应函数，从而得到极值的统计特征，如n次观测中的众数值及极值超过某特定值的概率。实际应用中，常以船舶的营运时间(或使用寿命)代替观测次数n，且首先给出极值超过某值的概率值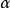，从极值的累积分布函数求得船舶在给定的营运时间中，超越率为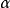的极值，以此值作为设计的参考值。若在上述分析中同时计入由于颤振、弹振等动载荷产生的附加弯矩的极值统计计特性和在静水中最大的弯知值，就可得到相应的船舶总纵弯的极值统计特征以及超越率为的极值2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所