[科普中国]-Gross-Pitaevskii方程

Gross–Pitaevskii 方程（以Eugene P. Gross命名与Lev Petrovich Pitaevskii) 描述了全同玻色子量子体系的基态，其中使用了Hartree-Fock近似与赝势相互作用模型。

定义Gross–Pitaevskii 方程（以Eugene P. Gross命名1与Lev Petrovich Pitaevskii) 描述了全同玻色子量子体系的基态，其中使用了Hartree-Fock近似与赝势相互作用模型。

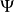在Hartree-Fock近似中，N个玻色子体系的总波函数为单粒子波函数之积

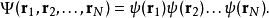其中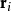为第i个玻色子的坐标。

赝势模型下的哈密顿量为

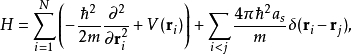其中m为玻色子质量，V为外势场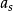，为玻色子-玻色子散射长度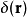，为狄拉克δ函数。

如果单粒子波函数满足Gross-Pitaevski方程，

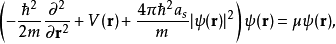则总波函数在归一化条件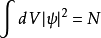下可以使赝势模型哈密顿量的总能量最小。

Gross-Pitaevski方程是描述玻色-爱因斯坦凝聚单粒子波函数的模型方程。它有类似金兹堡－朗道方程的形式，也会被称为非线性薛定谔方程.

玻色-爱因斯坦凝聚(BEC) 是处于同一量子态的玻色气体可以由同一个波函数进行描述。单个粒子可有单粒子波函数描述。真实气体中粒子相互作用包含在相应的多体薛定谔方程当中。当气体中粒子间距大于散射长度（即所谓的稀薄极限）时，真实的相互作用势就可以被替换为赝势。Gross-Pitaevskii方程的非线性来源于粒子间的相互作用。当把方程中相互作用的耦合常数设为零时，非线性消失，方程以描述单粒子在势阱中的单粒子薛定谔方程的形式出现。

方程形式Gross-Pitaevskii方程的形式类似于一般薛定谔方程，但是多出一个相互作用项。耦合常数{\displaystyle g}正比于两个相互作用玻色子间的散射长度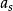

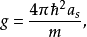其中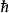为约化普朗克常数。能量密度为

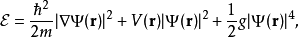其中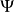为波函数，V为外部势场。 对于体系内粒子数守恒的不含时Gross–Pitaevskii方程

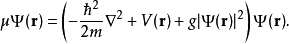其中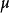为化学势。化学势是从粒子数与波函数间的关系中得到的

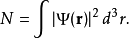从不含时Gross-Pitaevskii方程中，我们可以求得各种外势场中玻色爱因斯坦凝聚的内部结构（例如，谐振子势阱）。

含时Gross-Pitaevskii方程为

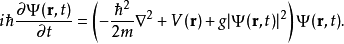利用含时Gross–Pitaevskii方程人们可以研究玻色爱因斯坦凝聚的动力学问题。

方程解鉴于Gross–Pitaevskii方程为非线性偏微分方程，一般很难求得解析解，大多数求解应用近似方法。

精确解**（1）自由粒子**

最简单的情况是描述自由粒子，外势场，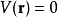

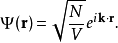
该解常被称为Hartree解。尽管它满足Gross–Pitaevskii方程，由于相互作用，其能谱中含有间隙

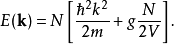
根据Hugenholtz–Pines定理，2含斥力相互作用的玻色气体并无能量间隙。

（2）孤子

一维孤子可以构成玻色爱因斯坦凝聚，取决于相互作用是引力还是斥力，形成亮孤子或暗孤子。两种孤子都是均匀密度背景下的定域扰动。如若相互作用是斥力形式的， g>0，Gross–Pitaevskii方程的可能解为，

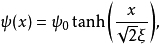其中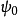为凝聚态波函数在无穷远处的值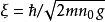，为相干长度。此解代表暗孤子，它描述在空间上原本均匀分布的密度出现了缺失。暗孤子是一种拓扑缺陷，因为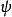在经过原点处符号发生翻转。这对应了数学上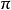的相移。

对于g