混合效应方差分析(Mixed-effect analaysis of variance)是固定效应方差分析和随机效应方差分析的混合,方差分析中主要有三种模型:依照因子的特性不同而有三种型态,固定效应方差分析(fixed-effect analysis of variance)、随机效应方差分析(random-effect analysis of variance)与混合效应方差分析(Mixed-effect analaysis of variance)。
方差分析在统计学中,方差分析(ANOVA)是一系列统计模型及其相关的过程总称,其中某一变量的方差可以分解为归属于不同变量来源的部分。其中最简单的方式中,方差分析的统计测试能够说明几组数据的平均值是否相等,因此得到两组的T检定。在做多组双变量T检定的时候,错误的概率会越来越大,特别是第一型错误,因此方差分析只在二到四组平均值的时候比较有效。
在方差分析的基本运算概念下,依照所感兴趣的因子数量而可分为单因子方差分析、双因子方差分析、多因子方差分析三大类1;依照因子的特性不同而有三种型态,固定效应方差分析(fixed-effect analysis of variance)、随机效应方差分析(random-effect analysis of variance)与混合效应方差分析(Mixed-effect analaysis of variance),然而第三种型态在后期发展上被认为是Mixed model的分支。
相关比较方差分析主要有三种模型:即固定效应模型(fixed effects model),随机效应模型(random effects model),混合效应模型(mixed effects model)。所谓的固定、随机、混合,主要是针对分组变量而言的。
固定效应方差分析固定效应方差分析表示仅打算比较已选中几组。例如,想比较3种药物的疗效,目的是为了比较这三种药的差别,不想往外推广。这三种药不是从很多种药中抽样出来的,不想推广到其他的药物,结论仅限于这三种药。“固定”的含义正在于此,这三种药是固定的,不是随机选择的。
随机效应方差分析随机效应方差分析表示比较不仅是已选中的几组,而且想通过这几组的比较,推广到他们所能代表的总体中去。例如,想知道是否名牌大学的就业率高于普通大学,选择了北大、清华、北京工商大学、北京科技大学4所学校进行比较,但目的不是为了比较这4所学校之间的就业率差异,而是为了说明他们所代表的名牌和普通大学之间的差异。因此结论不会仅限于这4所大学,而是要推广到名牌和普通这样的一个更广泛的范围。“随机”的含义就在于此,这4所学校是从名牌和普通大学中随机挑选出来的。
混合效应方差分析混合效应方差分析即是固定效应方差分析与随机效应方差分析的综合,就是既有固定的因素,也有随机的因素。此种混合效应绝对不会出现在单因子方差分析中,当双因子或多因子方差分析同时存在固定效应与随机效应时,此种模型便是典型的混合型模式。
模式假设方差分析之统计分析假设通常会依照各种模式型态不同而有差异,但广义而言,方差分析一共有三大前提假设2:
1.各组样本背后所隐含的族群分布必须为正态分布或者是逼近正态分布。
2.各组样本必须独立。
3.族群的方差必须相等。
总变量(TSS):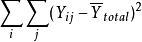 。
。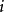 为组别(
为组别(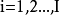 ),
),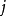 为观测值个数(
为观测值个数(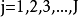 ),
),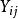 为第
为第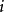 组第
组第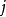 个观测值,
个观测值,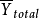 为所有观测值的平均数。
为所有观测值的平均数。
组间变异量(BSS):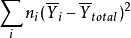 。
。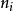 为i组内观测值总数,
为i组内观测值总数,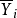 为第i组的平均数
为第i组的平均数
组内变异量(WSS):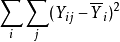 。
。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国