[科普中国]-常态分布曲线

常态分布曲线是一种对称的钟形曲线，具有均数等于0，标准差等于1的特点，从而使标准分数在实际运用时非常有用。

背景常态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学家研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。但现今德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。这要到20世纪正态小样本理论充分发展起来以后。拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。这是历史上第一次提到所谓“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年，海根（G.Hagen）在一篇论文中正式提出了这个学说1。

其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的“元误差” 之和，每只取两值，其概率都是1/2，由此出发，按狄莫佛的中心极限定理，立即就得出误差（近似地）服从正态分布。拉普拉斯所指出的这一点有重大的意义，在于他给误差的正态理论一个更自然合理、更令人信服的解释。因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一（算术平均的优良性，误差的正态性） 为出发点。但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义。

定义常态分布又称高斯分布，一般研究变量，常会呈现常态分布或近似常态分布，如身高，体重，收入，支出等等。常态分布曲线是一种对称的钟形曲线，具有均数等于0，标准差等于1的特点，从而使标准分数在实际运用时非常有用。

应用例如一场考试中成绩的判定，知道了常态分布曲线的Z分数，就能立刻知道该分数是在均数以上还是在均数以下。又因为标准分数是根据标准差求得的，知道了标准分数也就知道了它出现的概率。比如，在整个常态分布中，有34%的分数位于从均数到1个标准差的区域内，16%的分数位于分布的两端超出1个标准差的区域，大于2个标准差的分数只占2.5%2。

常态分布可以表示一个人的的得分在一个团体中的相对地位，可以在使用百分等级之外，选择使用〝标准分数〞：Z分数和T分数。(也就是将原始分数转换为一种以平均数为基准，以标准差为单位的距变数。以标准分数的优点来说：可以直接比较某生在不同考试中的相对地位或不同考生在不同考试中的相对地位。3

实现过程常态分布曲线的实现方法有多种，这里介绍常用的一种方法：利用Excel表格实现。

因为是标准正太分布，即μ=0，σ=1，做曲线图按以下步骤：
1.在A1输入公式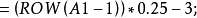
2.在B1输入公式
3.下拉复制上面的两个公式分别到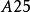 和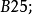

4.以A列为X轴，B列为Y轴插入“XY散点图”，选择散点图的类型为“带平滑线的散点图”

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所