[科普中国]-梳排序

**梳排序（Comb sort）**是一种由Wlodzimierz Dobosiewicz于1980年所发明的不稳定排序算法，并由Stephen Lacey和Richard Box于1991年四月号的Byte杂志中推广。梳排序是改良自泡沫排序和快速排序，其要旨在于消除乌龟，亦即在数组尾部的小数值，这些数值是造成泡沫排序缓慢的主因。相对地，兔子，亦即在数组前端的大数值，不影响泡沫排序的性能。

在泡沫排序中，只比较数组中相邻的二项，即比较的二项的间距（Gap）是1，梳排序提出此间距其实可大于1，改自插入排序的希尔排序同样提出相同观点。梳排序中，开始时的间距设置为数组长度，并在循环中以固定比率递减，通常递减率设置为1.3。在一次循环中，梳排序如同泡沫排序一样把数组从首到尾扫描一次，比较及交换两项，不同的是两项的间距不固定于1。如果间距递减至1，梳排序假定输入数组大致排序好，并以泡沫排序作最后检查及修正。

介绍**梳排序（Comb sort）**是一种由Wlodzimierz Dobosiewicz于1980年所发明的不稳定排序算法，并由Stephen Lacey和Richard Box于1991年四月号的Byte杂志中推广。梳排序是改良自泡沫排序和快速排序，其要旨在于消除乌龟，亦即在数组尾部的小数值，这些数值是造成泡沫排序缓慢的主因。相对地，兔子，亦即在数组前端的大数值，不影响泡沫排序的性能。

在泡沫排序中，只比较数组中相邻的二项，即比较的二项的间距（Gap）是1，梳排序提出此间距其实可大于1，改自插入排序的希尔排序同样提出相同观点。梳排序中，开始时的间距设置为数组长度，并在循环中以固定比率递减，通常递减率设置为1.3。在一次循环中，梳排序如同泡沫排序一样把数组从首到尾扫描一次，比较及交换两项，不同的是两项的间距不固定于1。如果间距递减至1，梳排序假定输入数组大致排序好，并以泡沫排序作最后检查及修正。1

排序算法在计算机科学与数学中，一个排序算法（英语：Sorting algorithm）是一种能将一串数据依照特定排序方式进行排列的一种算法。最常用到的排序方式是数值顺序以及字典顺序。有效的排序算法在一些算法（例如搜索算法与合并算法）中是重要的，如此这些算法才能得到正确解答。排序算法也用在处理文字数据以及产生人类可读的输出结果。基本上，排序算法的输出必须遵守下列两个原则：

输出结果为递增序列（递增是针对所需的排序顺序而言）

输出结果是原输入的一种排列、或是重组

虽然排序算法是一个简单的问题，但是从计算机科学发展以来，在此问题上已经有大量的研究。举例而言，冒泡排序在1956年就已经被研究。虽然大部分人认为这是一个已经被解决的问题，有用的新算法仍在不断的被发明。1

递减率递减率的设置影响着梳排序的效率，原作者以随机数作实验，得到最有效递减率为1.3的。如果此比率太小，则导致一循环中有过多的比较，如果比率太大，则未能有效消除数组中的乌龟。

亦有人提议用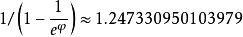作递减率，同时增加换算表协助于每一循环开始时计算新间距。

因为编程语言中乘法比除法快，故会取递减率倒数与间距相乘，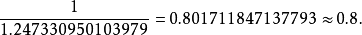

变异形式梳排序-11设定递减率为1.3时，最后只会有三种不同的间距组合：(9, 6, 4, 3, 2, 1)、(10, 7, 5, 3, 2, 1)、或 (11, 8, 6, 4, 3, 2, 1)。实验证明，如果间距变成9或10时一律改作11，则对效率有明显改善，原因是如果间距曾经是9或10，则到间距变成1时，数值通常不是递增序列，故此要进行几次泡沫排序循环修正。加入此指定间距的变异形式称为梳排序-11(Combsort11)。2

混合梳排序和其他如同快速排序和合并排序，梳排序的效率在开始时最佳，接近结束时，即进入泡沫排序时最差。如果间距变得太小时(例如小于10)，改用诸如插入排序或鸡尾酒排序等算法，则可提升整体效能。

此方法的最大好处是不再需要检查有否进行过交换程序以将排序循环提早结束。1

伪代码梳排序程序（以array作输入） gap = array的长度//设定开始时的间距 当gap > 1或swaps = 1时执行回圈//代表未完成排序 gap =取「gap除以递减率」的整数值//更新间距 swaps = 0 //用以检查阵列是否已在递增形式，只限gap=1时有效 //把输入阵列「梳」一次 i = 0到(array的长度- 1 - gap)来执行回圈//从首到尾扫描一次；因为阵列元素的编号从0开始，所以最后一个元素编号为长度-1 如果array[i] > array[i+gap] 把array[i]和array[i+gap]的数值交换 swaps = 1 //曾作交换，故此阵列未必排序好 如果结束 回圈结束 回圈结束程序结束算法实现C语言实现：2

void comb_sort(int* data, int n){const double shrink = 1.25;int i, delta = n, noswap = 0;while(!noswap){for(noswap = 1, i = 0; i + delta data[i + delta]){data[i] ^= data[i + delta];data[i + delta] ^= data[i];data[i] ^= data[i + delta];noswap = 0;}if(delta > 1){delta /= shrink;noswap = 0;}}}动作原理假设输入为

8 4 3 7 6 5 2 1

目标为将之变成递增排序。因为输入长度=8，开始时设置间距为8/1.3≒6，则比较8和2、4和1，并作交换两次。

84 3 7 6 521

243 7 6 5 81

2 1 3 7 6 5 8 4

第二次循环，更新间距为6/1.3≒4。比较2和6、1和5，直至7和4，此循环中只须交换一次。

2 1 376 5 84

2 1 3 4 6 5 8 7

接下来的每次循环，间距依次递减为3 → 2 → 1，

间距=3时，不须交换

2 1 3 4 6 5 8 7

间距=2时，不须交换

2 1 3 4 6 5 8 7

间距h=1时，交换三次

2****13 4 6 5 8 7

1 2 3 46****58 7

1 2 3 4 5 68****7

1 2 3 4 5 6 7 8

上例中，共作了六次交换以完成排序。2

参看泡沫排序，梳排序的基本，较慢的算法。

鸡尾酒排序，或双向泡沫排序，一样解决了泡沫排序中的乌龟问题。

本词条内容贡献者为:

李岳阳 - 副教授 - 江南大学