[科普中国]-贝内迪克特-韦德-鲁宾方程

贝内迪克特-韦德-鲁宾方程又叫BWR方程(Benedict-Webb-Rubin equation)是由M.本尼特、G.B.韦布和L.C.鲁宾于1940年提出的应用于非极性化合物的纯流体维里状态方程。

简介及表达式BWR方程：

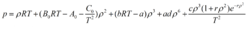
式中，ρ=1/Vm；

A0、B0、C0、a、b、c、d和r均为特征参数，由实验回归而得。

该方程对烃类化合物较为适用，是第一个能同时应用于汽液两相的状态方程。1970年K.E.斯塔林对BWR方程作了改进，提出包括11个参数的BWRS方程， 其应用范围比BWR方程更广。1

BWR方程的应用BWR方程可用于计算低温轻烃混合物的热力学性质，对于含H2， N2， Ar， CO2等轻烃混合物用BWR状态方程来计算气液平衡和热力学性质在100°K以上是能得到满意的结果，并能满足工程计算精度的要求。对于含He和NH3的轻烃混合物在含量不太高的情况下亦能得到较为满意的结果。2

通常将高于临界温度和临界压力的物质状态称之为流体状态。由于超临界流体兼有液体和气体的双重性，具有很强的溶解能力和良好的流动、输运性质。基于这些特性，超临界流体被广泛地应用于食品、医药、生物工程、化工、环保、超临界清洗等诸领域，而在超临界流体中研究和应用最多的体系就是超临界C02。

这里就将多参数的BWR方程应用于超临界CO2流体，采用非线性最小二乘法，精选参与拟合的实验数据和初始参数，拟合出适用于温度为310~600 K、压强为7.5~30.0 MPa范围的超临界CO2的有关参数，进而做了压强p的回代计算，同时将所有的数据点以等温线的形式绘制成右图。3

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所