[科普中国]-levinson算法

Levinson算法有时也称“莱文逊算法”，是一种计算自回归模型参数的方法。Levinson算法是一种迭代算法，而且Levinson算法在任何域上都成立。特别是，它在复数域上也成立。然而，在实际应用中，对称的Toeplitz 矩阵并不经常出现，更常见的是厄尔米特Toeplitz矩阵。在这种情况下Levinson算法也成立，只要在计算中的适当的点上取复共轭就行了。可以很容易对这种情况进行重新推导。有时可用一种叫做Durbin算法的更好的算法来代替Levinson算法1。

基本介绍设 {xt} 为观察序列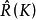，， K=0， 1， …为其样本协方差函数。若用n阶自回归模型对{xt}进行拟合，通过求解n阶Yule-Walker方程

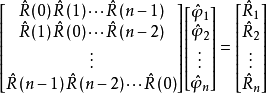可得到自回归参数的矩估计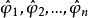，拟合线差为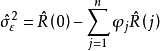：。将两式合并写成矩阵形式：

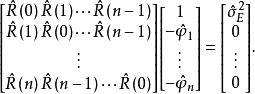
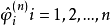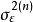在实际计算时，经常用阶数依次递增的自回归模型对数据序列{xt}进行拟合，然后按照某种准则挑选最适宜的模型阶数。上式中的自回归参数和残差实际上和AR的阶数n有关， 记作：和。Levinson算法就是以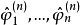和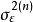递推算出的阶数增大为n+1的相应参数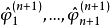和。

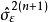Levinson算法递推步骤Levinson算法递推步骤如下：

令

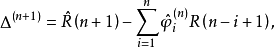
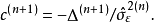参数估计式为：

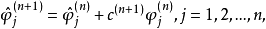
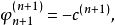
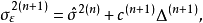放值为

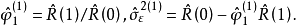这个算法随着自回归模型阶数的递增依次给出相应模型的自回归参数和残差的估计值，该算法的运算是为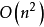，而通常求解Yule-walker方程的计算量为。

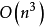本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所