[科普中国]-高斯—牛顿迭代法

高斯一牛顿迭代法(Gauss-Newton iteration method)是非线性回归模型中求回归参数进行最小二乘的一种迭代方法，该法使用泰勒级数展开式去近似地代替非线性回归模型，然后通过多次迭代，多次修正回归系数，使回归系数不断逼近非线性回归模型的最佳回归系数，最后使原模型的残差平方和达到最小。其直观思想是先选取一个参数向量的参数值β，若函数ft(Xt，β)在β0附近有连续二阶偏导数，则在β0的邻域内可近似地将ft(Xt，β)看作是线性，因而可近似地用线性最小二乘法求解1。

基本思想高斯-牛顿迭代法的基本思想是，使用泰勒级数展开式去近似地代替非线性回归模型，然后通过多次迭代，多次修正回归系数，使回归系数不断通过通近非线性回归模型的最佳回归系数，最后使原模型的残差平方和达到最小2。

一般步骤高斯-牛顿法的一般步骤如下所示2。

(1) 初始值的选择。其方法有三种：

一是根据以往的经验选定初始值；

二是用分段法求出初始值；

三是对于可线性化的非线性回归模型，通过线性变换，然后施行最小平方法求出初始值2。

(2)泰勒级数展开式。设非线性回归模型为

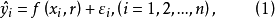其中: r为待估计回归系数，误差项。

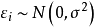设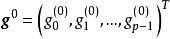为待估回归系数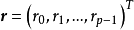的初始值，将式(1)在g0点附近作泰勒展开，并略去非线性回归模型的二阶及二阶以上的偏导数项，得

将式(2)代人式(1)，则

移项，有

令

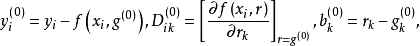则

用矩阵形式表示，上式则为

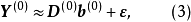其中

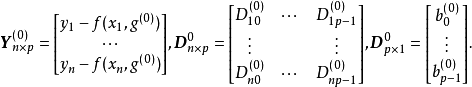
(3)估计修正因子。用最小平方法对式(3)估计修正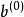

则

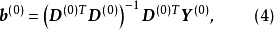设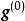为第一个迭代值，则。

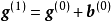(4)精确度的检验。设残差平方和为

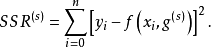其中，s内重夏迭代次数。对于给定的允许误差率K，当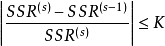时，否则，对式(4) 作下一次迭代。

(5)重夏迭代。重夏式(4)，当重夏迭代s次吋，则有

修正因子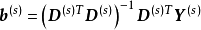，第(s+1)次迭代值。

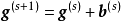本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所