当采用指数平滑方法进行预测时,一般情况下平滑系数α为一常数。当预测的结果与实际结果之间的误差不大时可以认为是正常的,但如果超出了一定的范围,说明原来的平滑系数需要加以调整、因此需要建立预测的控制。一些人提出了选择平滑系数的规则,规定了低、中、高三个平滑系数,根据预测的误差情况来加以调整,这种根据不同预测结果来调整平滑系数的指数平滑法称作自适应指数平滑1。
基本介绍针对时间序列数据依据过去的变化规律,推断今后变化的可能性及其变化趋势、变化规律,自适应指数平滑方法就是其中的一种代表性方法。
自适应指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均2。
自适应参数的求取一次指数平滑法的基本公式是:
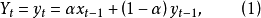 式中,
式中,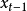 和
和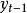 为t-1时刻的实测值与预测值;
为t-1时刻的实测值与预测值;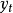 是t时刻的平滑值;
是t时刻的平滑值;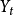 是t时刻的预测值;
是t时刻的预测值;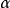 为平滑系数,又称加权因子,其取值范围为[0,1]。
为平滑系数,又称加权因子,其取值范围为[0,1]。
 的大小表明了修正幅度,
的大小表明了修正幅度, 值越大修正幅度越大,既代表了预测模型对时间序列数据变化的反应速度,又体现了预测模型修正误差的能力。自适应指数平滑模型进行预测时
值越大修正幅度越大,既代表了预测模型对时间序列数据变化的反应速度,又体现了预测模型修正误差的能力。自适应指数平滑模型进行预测时 值并非预先根据经验给定,而是对交通流时变过程中引入动态权重因子
值并非预先根据经验给定,而是对交通流时变过程中引入动态权重因子 2。
2。
假设在t时刻指数平滑预测误差 为
为
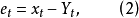 取加权平均
取加权平均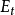
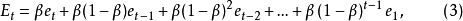 其递推形式为
其递推形式为
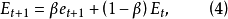 同时t时刻绝对平滑误差为
同时t时刻绝对平滑误差为
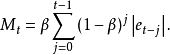 自适应参数
自适应参数 的求取步骤如下:
的求取步骤如下:
(1)设置模型初始值:初值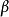 的选取,由于经过多次平滑递推计算,其值对预测产生的影响将会越来越小,因此只需取经验值(0.1或0.2)即可。初值
的选取,由于经过多次平滑递推计算,其值对预测产生的影响将会越来越小,因此只需取经验值(0.1或0.2)即可。初值 一般取为
一般取为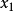 ,相应地
,相应地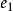 和
和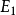 取为0,初值M1一般取为经验值0.1
取为0,初值M1一般取为经验值0.1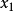 。
。
(2)求综合预测误差
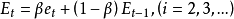
(3)求绝对平滑误差
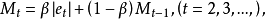
(4)得到自适应权重参数

(5)求出自适应平滑参数后,就可以用动态的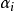 ,代替恒定的
,代替恒定的 ,从而得到自适应指数平滑预测模型如下:
,从而得到自适应指数平滑预测模型如下:
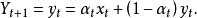
上述方法具有建模简单,没有参数辨识等烦琐过程,对历史数据依赖性比较小的特点,这就从根本上保证了算法的快速性,因而能够确保估计算法的实时性2。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国