[科普中国]-谱熵

谱熵（spectral entropy ）这一概念描述了功率谱和熵率之间的关系。研究表明，由自回归模型估计出的谱具有最大的谱熵，因而是一种理想的求谱方法，称为最大熵谱估计法，简称MEM，所得的谱称为最大熵谱。

基本概念设yt是一个稳定的因果系统的输入，该系统的传递函数为G (B)(它在单位园内无极点)，，xt为系统的平稳输出，则可以证明，系统的输入与输出的熵率之间的关系为。这一关系在时间序列中应用最多的是输入{yt}为零的值白噪声，方差为，这时系统的传递函数，而白噪声的熵率为，由此得到{xt}的熵率为。以白噪声为输入的线性平稳系统恰是时间序列ARMA模型，上面的关系式反映了{xt}的谱密度和它的熵率之间的关系。式中右边第一项是常数，比较hx的大小等价于比较第二项积分的大小，因此称为序列{xt}的谱熵，其含意即是用功率谱来表示的熵1。

熵谱与极大熵谱估计估计平稳随机过程功率谱密度的方法，这种方法在外推时能使自相关函数在未知点的取值具有最大统计自由度。J.P.伯格于1967年首先提出这种方法并把它称为极大熵谱估计。极大熵谱估计最初应用于地球物理学领域地震记录数据的分析，后来在雷达、声纳、图像处理、语言分析以及生物医学等领域都有广泛的应用。

在统计学中，熵是对各种随机试验不确定程度的一种度量。概率分布的熵越大、试验的可能结果越不确定。伯格的思想是要在外推相关函数的每一步，都既能保证相关函数的已知部分不变，又能在新增加外推值之后使概率分布具有最大的熵；也就是在每步外推时不对未知点处自相关函数取值施加任何限制（即其取值具有最大统计自由度，不对它强加任何条件）。极大熵谱估计的这种特点能克服传统的功率谱估计方法分辨率不高的弱点。在理论上，过程的功率谱是自相关函数的傅里叶变换。传统的功率谱估计方法是将样本自相关函数乘以某种窗函数(即对自相关函数加权)，然后再作傅里叶变换。窗函数可以增加谱估计的稳定性并减少谱的泄漏，但窗函数会限制谱的分辨力。传统方法存在的问题实际上是由于它把没有观测到的数据（或其自相关函数）都看作为零，同时对已知部分的信息加以人为修改（加权）而引起的。而极大熵谱估计对已知的最大迟延以外的自相关函数进行合理的外推，因而能提高所求功率谱的分辨力，特别是在已知数据量较少时，其效果比传统方法更优。

极大熵谱估计是以极大熵为准则的谱估计，设f(ω)是平稳序列xt(t=0，±1，…)的正规化谱(密度函数)，称

为平稳序列xt的谱熵。假定xt的前m+1个自协方差函数值

已知，在约束

下，使得谱熵I(f)达到极大值，以此作为准则，所得到的估计称为极大熵谱估计。给定观察值x1，x2，…，xT，利用样本自协方差函数γk代替自协方差函数，求解上述变分问题可得到极大熵谱估计。而此问题实质上归于求解尤尔-沃克方程

令

最后得出极大熵谱估计

所以又称此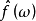为谱的矩估计2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所