复系数多项式因式分解定理:每个次数大于等于1的复系数多项式在复数域上都可以唯一地分解成一次因式的乘积。
代数基本定理每个次数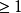 的复系数多项式在复数域中有一个根.1
的复系数多项式在复数域中有一个根.1
推论1: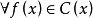 ,若
,若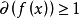 ,则存在
,则存在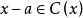 ,使得
,使得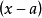 |
|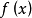
即代数基本定理可以等价地叙述为:每个次数的复系数多项式在复数域上一定有一个一次因式。
推论2:复数域上不可约多项式只有一次多项式。即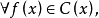 若
若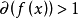 ,则
,则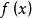 可约。
可约。
复系数多项式因式分解定理及推论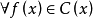 ,若
,若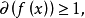 则
则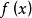 在复数域上可唯一分解成一次因式的乘积。1
在复数域上可唯一分解成一次因式的乘积。1
推论1: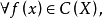 若
若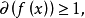 则
则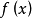 在复数域上具有标准分解式。
在复数域上具有标准分解式。
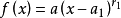
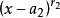
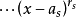 其中
其中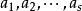 是不同的复数,
是不同的复数,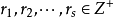
推论2:每个n次复系数多项式恰好有n个根(重根按重数计算)。
应用举例求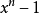 在复数域上的标准分解式
在复数域上的标准分解式
证:由定理推论2得,在复数域上原式有n个根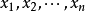
因此,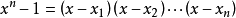 ,其中
,其中
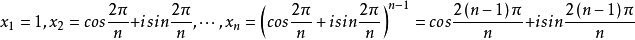
本词条内容贡献者为:
朱坤平 - 副教授 - 华东理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国