[科普中国]-不等概率抽样

不等概率抽样是指在抽取样本之前给总体的每一个单元赋予一定的被抽中概率。不等概率抽样分为放回与不放回两种情况。有放回的不等概率中，最常用的是按总体单元的规模大小来确定抽选的概率。不放回的不等概率抽样，是指在抽样的过程中被抽中的单元不能再被抽中，因此在抽取了第一个单元之后，余下的N-1的单元中再以什么样的概率抽选就比较复杂。接着抽取第三和第四个单元时就面临更复杂的问题，因此抽样的实施比较困难。这种抽样要求做到第j个单元入样概率为πj，在样本容量为n时所有N个单元的入样概率之和就应等于n1。

不等概率抽样的概率与特点简单随机抽样中，总体中的每个单元具有同样的入样概率，它们是等概率抽样，在分层随机抽样中，层内单元是按简单随机抽样抽取的，因此，它们也是等概率抽样。等概率抽样的特点是总体中每个单元地位相同，在抽样时对每个单元采取“不偏不倚”的态度。

与等概率抽样对应的另一类方法是不等概率抽样，也就是在抽样前赋予总体每个单元一个入样概率，当然这个人样概率是不相同的，否则抽样就成为等概率的抽样。

当总体单元之间差异不大时，简单随机抽样也是简便的、有效的。例如，对家庭消费支出的调查中，以家庭为抽样单元，由于家庭之间的差异不是很大，因此用简单随机抽样也是有效的2。

当总体单元之间差异非常大时，简单随机抽样效果并不好。例如，对船舶运输量进行调查时，以船舶为抽样单元，则有的是从事远洋运输的万吨巨轮，更多的是从事内河河网运输的上百吨乃至几十吨小船，这对，简单随机抽样的效果肯定不好。

出现总体单元差异特别大的情况时，通常是牺牲“简单”来提高抽样效率的。一种做法是将总体单元按规模(大小)分层，对较大单元的层抽样比定得高些，抽样比甚至是i00%，而较小单元的层抽样比定得低一些。另一种做法就是赋予每个单元与其规模(或辅助变量)成比例的入样概率，这样以来，大单元入样概率大，小单元入样概率小。

实际工作中，如果遇到下面几种情况，则可以考虑使用不等概率抽样。

1．样本单元在总体中所占的地位不一致。

例如上面所讨论的船舶等调查问题。

2．调查的总体单元与抽样总体单元不一致。

例如某大型单位准备对职工家庭进行调查，一种自然的办法就是以人事部门的职工花名册作为抽样框进行抽样，该单位有少数家庭两名职工在该单位工作，如果对职工进行简单随机抽样，则双职工家庭被抽中的概率大，而调查者希望对家庭进行等概率抽样。除了对抽样框进行整理，将双职工家庭中的一名成员从抽样框拿掉以外，可以对职工采用不等概率抽样，一种做法是对每名职工记录其家庭成员在该单位工作的人数，然后对每名职工按与人数成反比的概率进行抽样。

3．改善估计量。

不等概抽样可用于对估计量进行改善，例如简单随机抽样比率估计量是渐进无偏的，要使它成为无偏估计，只要每个大小为n的样本被抽中的概率与其辅助变量的和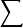成比例(如水野法)，则这时的比率估计就是无偏估计量，而这个样本并不是简单随机样本，而是一个不等概率抽样获得的样本2。

不等概率抽样的种类放回不等概率抽样每次在总体中对每个单元按入样概率进行抽样，抽取出来的样本单元放回总体，然后进行下一次抽样。这样的话，每次抽样过程都是对同一个总体独立进行的。放回不等概率抽样实施及推算过程相对来说比不放回的简单2。

不放回不等概率抽样每次在总体中对每个单元按入样概率进行抽样，抽取出来的样本单元不再放回总体，对总体中剩下的单元进行下一次抽样。不放回不等概率抽样的效率比放回时的效率高，但是不放回不等概率抽样的实施及推算过程比放回时复杂得多。

对于不放回不等概率抽样，样本的抽取可以有以下几种方法：

1．逐个抽取法

每次从总体未被抽中的单元中以一定的概率抽取一个样本单元，通常这个概率与已被抽中的样本单元有关。

2．重抽法

以一定的概率逐个进行放回抽样，如果抽到重复单元，则放弃所有抽到的样本单元，重新抽取，直至抽到规定的样本量且所有样本单元不重复。

3．全样本抽取法

对总体每个单元分别按一定概率决定其是否入样。这种方法的样本量是随机的，事先不能确定，而且它可能出现总体中全体单元都人样或全都未入样。

4．系统抽样法

将总体单元按某种顺序排列，将规定的入样概率汇总，根据样本量确定抽样间距k，在1～k产生一个随机数，并确定相应的初始单元，以后在总体中每隔忌个单元抽出一个作为样本单元2。

区域抽样区域抽样也称为面积抽样。这种方法主要用于以下的情形：区域或面积本身就是抽样单元，或者抽样单元的名单抽样框无法获得，但每个抽样单元只隶属于某个区域。例如，某县进行小麦产量调查时，将全县农田土地按易于划分的规则划分成地块(如利用沟渠、水渠、道路等地理特征自然隔离)。然后对地块进行抽样，对被抽中地块的小麦产量进行实割实测，从而推算全县的产量。由于地块的面积通常不相等，因此对地块的抽样可以是简单随机抽样，也可以按地块的面积进行不等概率抽样。

为此，需要对抽样框类型进行讨论。抽样框可以分为名单抽样框和区域抽样框。

名单抽样框由抽样单元组成。例如，某高校全体在校学生的花名册就是一个名单抽样框。又如，在工商管理部门登记的企业名册也是一个名单抽样框。

区域抽样框由定义明确的区域组成，而一个区域是由个体组成的。例如，我们对居民家庭进行某项调查时，可以利用地图编制各行政区的名单，或到街道办事处获得居委会的名单，这时的行政区及居委会都是由个体(居民户)组成的区域，又如将农田土地划分成地块。

一般来说，抽样调查的总体比较大，要编制全体抽样单元的名单往往很困难，而且也没有必要。这时比较容易的做法是通过对区域的划分，建立区域抽样框，然后对被抽中的区域进行调查，或者再编制下一阶段的抽样框。如果有必要，这个抽样框也可以是区域抽样框。

区域抽样框有以下主要优点：

1．容易定义和识别

区域抽样框很容易通过地图或行政区加以定义，而且能很清楚地识别。

2．比较稳定

区域相对来说比较稳定。例如，我们调查一个居民楼中的所有居民户，比利用居民户名单抽样框要容易得多，因为前者是稳定的，而后者可能在调查的时候已经搬迁。

3．容易操作，回答率较高

现场工作人员能很容易并清楚地识别和确定区域的界限，从而比较容易地找到样本单元，使回答率提高2。

多项抽样与PPS抽样设是一组概率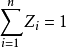，，按这组概率对总体中的N个单元进行放回抽样，每次抽中第i个单元的概率为，独立地进行这样的抽样n次，则这种不等概抽样为多项抽样。

特别地，如果每个单元有说明其大小或规模的度量M1，则

这时，每个单元在每次抽选中入样的概率与其单元规模的大小成比例，因而多项抽样称为放回的与单元规模大小成比例的概率抽样(sampling with probability proportional to size)，简称PPS抽样。

由于抽样是放回的，因此，某个单元可能在样本中出现多次，出现这种情况时，对这个单元的调查只进行一次，但计算时按抽中几次计算几次的原则进行2。

πPS抽样对于放回抽样，对总体参数的估计及其方差估计比较简单，但样本单元中可能有单元被抽中多次。直观上看，没有必要对同一个单元调查多次，因此放回抽样得到的样本代表性比不放回抽样差。类似于简单随机抽样的讨论，在同样样本量的条件下，放回抽样的估计量精度较低，尤其当抽样，比不能忽略时，称不放回的与单元大小成比例的概率抽样为πPS抽样2。

不等概率抽样的实施方法代码法在PPS抽样中，赋予每个单元与M1相等的代码数，将代码数累加得到M0，每次抽样都产生一个[1，M0]之间的随机数，设为m，则代码m所对应的单元被抽中。

如果Mi不是整数，则乘以某个倍数。对于一般的多项抽样，通常可以找到某个M0，使M0Z1为整数，每个单元赋予与M0Z1相等的代码数，然后进行抽样。

拉希里法令，即所有Mt中最大值，每次抽样都分别产生一个[1，N]之间的随机数i及[1，M*]之间的随机数m，如果Mt≥m则第i个单元被抽中；否则，重抽一组(i，m)2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所