[科普中国]-定理机器证明

定理机器证明是用计算机自动地进行推理和证明数学定理。又称为自动定理证明(ATP)。让机器去证明数学定理的想法，在17世纪G.W.Leibniz 创立数理逻辑时就产生了，但这一想法的真正实现，是在20世纪40年代计算机诞生以后。

简介从1956年A.Newell，J.C.Shaw,H.A.Simon发表他们的著名论文“逻辑理论机”算起，自动定理证明这个研究领域已经有近四十年的历史了。逻辑理论机是机械地模仿人类在证明命题逻辑定理时所用的推导过程。1959年 H.Gelernter 等人做出了几何定理证明机(GTM)。GTM能够证明直线图形中的大部分高中的考试题，而且运行时间也常常与高中学生做题的时间相当。1959年P.C.Gilmore设计了关于谓词演算的机械证明程序。在1958到1960年间王浩研究出关于命题演算和谓词演算的机械证明程序。1965年J.A.Robinson提出了归结原理。归结原理实质上是一条简洁的推理规则。使用这一条规则，对一阶逻辑中的任一个恒真公式，都将是可证的。L.Wos是最成功地实现归结系统的研究者之一，为此，他获得首次ATP奖。1972年左右，以L.Wos 为首的集体建立了一个以归结方法为主的自动推理系统AURA。这个系统对于解有限数学，线路设计，程序正确性验证及形式逻辑等领域中的疑难问题，提供了帮助。归结方法是ATP领域中第一类方法———逻辑方法的代表。

ATP领域中第二类方法———类人方法，有时也称为自然演绎或自然推导法。A.Newell等人的逻辑理论机就使用了类人方法。1966年美国麻省理工学院的L.Norton建造了一个系统ADEPT，该系统是一个关于群论的启发式定理证明系统，它使用了很多有效的启发式规则。这个系统的能力界限是能够证明：若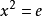，则群是交换群。

ATP领域中的第三类方法是所谓判定过程。判定过程是指: 判断一个理论中的某个公式的有效性。1978年，中国的吴文俊关于平面几何和微分几何的定理机 器证明方法(亦即吴方法) 被认为是ATP领域中判定方法的一个最好的结果。使用这个方法，在计算机上证明和发现了平面几何中一些有趣的定理。

下面用简单而直观的例子说明ATP领域中这三类方法。我们知道一个定理：若A成立，则B成立;还知道一个事实：A成立。欲证明一个结论：B也成立。我们想做的事，在数理逻辑中 ,相当于去证明公式：

(1)

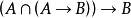
是一个定理，亦即证明公式(1)是恒真的。

第一种方法：归结方法是反驳方法，要证明公式(1)是恒真的，相当于证明公式(1)的否定是恒假的，亦即证明：

(2)

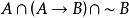
是恒假的(～B表示B的否定)。A和(A→B)归结得B，B和～B归结得恒假公式(即空子句)。因此，公式(2)是恒假的，所以公式(1)是恒真的，定理得证。

第二种方法：类人方法就是模仿人在证明定理时的思维过程，将原目标不断分解成易证的子目标，直到子目标都是(P→P)的形式。为了证 明公式(1)，只要能证明(A→ B)或者(( A→ B)→B)中的一个即可 (这称为自然演绎法中的“或分枝规则”)。(A→B)无法证明，考虑：

(3)

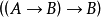
只要能证明(B→ B)和A即可(这称为“反向链规则”)。而(B→ B)可证，下面证明A使用定理(1)的前提，即是要证明：

(4)

对公式(4)再使用“或分枝规则”，只要能证明(A→A)或者((A→B)→A)中的一个即可，而(A→ A)可证，故式(4)可证，因此A可证，故式(3)可证，所以定理(1)可证。

第三种方法：判定方法不是直接去证明定理，而是去判定这个定理是否正确，对定理使用真值表法即可判定它是成立的。

上述三种方法较详细的论述可分别参见归结方法，自然演绎法，吴方法。

定理机器证明面对的是数学领域，这就决定了定理机器证明必然要面临巨大的困难。因此，从20世纪80年代开始，很多研究定理机器证明的学者，转向了使用简单推理就能获得成效的领域，从而诞生了人工智能中一个极为活跃的研究领域———自动推理。自动定理证明和自动推理在人工智能领域中越来越显出其重要性。1

方法举例①归结方法：归结是定理机器证明的一个重要方法，1965年由J.A.鲁宾逊建立。例如以P、Q、R、S分别代表四种陈述，-P表示P不真,P∨Q表示P和Q至少有一个为真。最简单的归结原理就是：由P∨Q和-P∨R可推出Q∨R。假定已知事实：-P∨-Q、Q∨R∨-S、P、S,欲证R成立。归结方法总是使用反证法，因此，假定要证的定理不成立，即假定-R。把P-∨-Q和Q∨R∨-S相归结得-P∨R∨-S,以此与-R归结得-P∨-S，再与P归结得-S,结果与S矛盾,故定理得证。

②自然推导：归结方法及其改进过于一般化，故效率不高。人在某一领域内证明定理是用自然推导法，即除一般的逻辑推导外还利用他在这一领域中的知识和经验。模仿人的这种自然推导法的最初成果是1963年A.纽厄尔、J.C.肖和H.A.西蒙的LT系统。另外，还有以归结方法与自然推导相结合的系统。

③判定方法：在较小的领域内找一个有效的判定方法来作定理证明也受到人们的重视。这方面最早的工作是A.塔斯基的初等代数和初等几何的判定方法。这种方法虽效率很低，但后来又有人作了不少改进。王浩给出命题逻辑的一个很有效的判定方法。吴文俊提出的关于初等几何和微分几何的判定方法也是很成功的。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学