[科普中国]-高次方程

高次方程又称为整式方程，未知数次数最高项次数高于2次的方程均可称为高次方程。

背景伽罗华（Galois，1811——1832），法国数学家。

伽罗华15岁进入巴黎有名公立中学学习，偏爱数学。后来想进工科大学，两次落榜只进一所代等的预备学校，此时，他专攻五次方程代数解法。第一年写了四篇文章，1828年，17岁的伽罗华写了《关于五次方程的代数解法问题》等两篇论文送交法国科学院，但被柯西（Cauchy,1789——1875）遗失，后来，他又把一篇文章送给傅利（Fourier，1768——1830）。不久，傅利就去世了，也就不了了之。1831年，伽罗华完成了《关于用根式解方程的可解性条件》一文，院士普阿松（Poisson，1781-1840）的审查意见却是“完全不能理解”，予以退回。伽罗华不幸因决斗受重伤于1832年5月31日离世，时年不满21岁，在决斗前夜，他深知为女友决斗而死毫无意义，但又不甘示弱，当晚他精神高度紧张和极度不安，连呼“我没有时间了！”匆忙之中，把他关于方程论的发现草草写成几页说明寄给他的朋友，并附有如下一段话：“你可以公开地请求雅可比（Jacobi）或高斯，不是对于这些定理的真实性而是对于其重要性表示意见，将来我希望有人会发现这堆东西注释出来对于他们是有益的。”

随着时间的推移，伽罗华的卓越贡献越来越为数学家所认识。他的学术思想对近代数学产生了深远的影响：他开创的群论逐渐渗透到数学其它分支，以及结晶学，理论物理学等领域，群论给这些领域提供了有力的数学工具比如用群论证明了结晶体的类型只有230种，群论为诸如方程的根，晶体的结构，空间变换，基本粒子的对称性等课题的研究提供统一的方法。到20世纪，群论的概念在整个数学中占有重要的地位，成为现代数学的基础之一1。

但伽罗华只给出了能否根式求解的判别方法，没有给出具体的求解方法。通常情况下求精确值比较困难，工程上只需要求解近似根即可，常用的求解近似根的方法有牛顿切线法，牛顿割线法，二分法，劈因子法，林士谔-赵访熊法等。

定义及形式定义：

整式方程未知数次数最高项次数高于2次的方程，称为高次方程2。

高次方程的一般形式为：

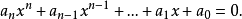
等式两边同时除以最高项系数，得：

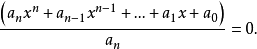
所以高次方程一般形式又可写为

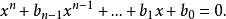
解法解法思想是通过适当的方法，把高次方程化为次数较低的方程求解。对于5次及以上的一元高次方程没有通用的代数解法和求根公式（即通过各项系数经过有限次四则运算和乘方和开方运算无法求解），这称为阿贝尔定理。 换句话说，只有次数为2,3,4次方程才有求根公式。但并不排除对一些特殊的高次方程有根式解，比如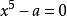 有根式解2。

通过适当的方法，把高次方程化为次数较低的方程求解．

按这个高次方程的形式

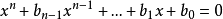，那么有所有根相加等于系数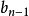的相反数，所有根两两相乘再相加等于系数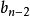，所有根三三相乘再相加等于系数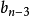的相反数，依次类推，直到所有根相乘，等于。

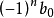例子一元三次方程的求根公式用通常的演绎思维是作不出来的，用类似解一元二次方程的求根公式的配方法只能将型如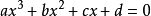的标准型一元三次方程形式化为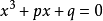的特殊型。

一元三次方程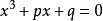，判别式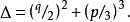

【卡尔丹公式】

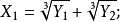
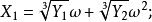
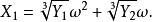
其中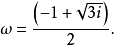

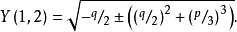
一般式一元三次方程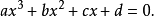

令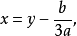代入上式，

可化为适合卡尔丹公式求解的特殊型三次方程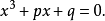

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学