[科普中国]-希腊拉丁方

希腊拉丁方亦称“正交拉丁方”，试验设计的一种。由两个互相正交的拉丁方重叠而成。本质上可以与正交表互变。三阶希腊拉丁方可用于四因子，每个因子各有三个水平的析因，其中行、列位置的拉丁字母、希腊字母各可代表一个因子。每个因子的水平与其他三个因子的任一水平的组合， 出现并只出现一次。其基本假设同拉丁方。不存在阶数为6的希腊拉丁方。多于三阶的正交拉丁方称为超希腊拉丁方。1

基本介绍由两个同阶拉丁方叠合而得到的拉丁方，称做希腊-拉丁方。把两个拉丁方

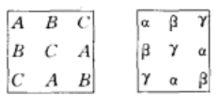
相叠合，得到一个新的方阵

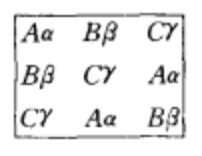
它仍然是一个拉丁方；因此是希腊一拉丁方。并非任何两个拉丁方叠合都能得到拉丁方，但是两个相互正交的拉丁方相叠合一定是希腊-拉丁方2。

称两个同阶拉丁方为正交的，如果两个拉西方叠合得到的方阵仍然是拉丁方，即两个拉丁方的字母每一种可能的两两组合，在所得方阵中的各行和行列中都恰好出现一次。两个正交拉丁方相叠合所得拉丁方称做“希腊-拉丁方”。例如，下面的三个四阶拉丁方是两两正交的。

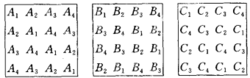
可以证明，对于任意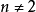 和6，都存在相互正交的拉丁方；在Nn个n阶拉丁方中，最多有n-1个两两正交的拉丁方。假如恰有n-1个n阶正交拉丁方，则称它们构成正交拉丁方完全系；当 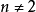为素数或某个素数幂时，都存在n-1个两两正交的拉丁方，它们构成正交拉丁方完全系。对于不同的n≥3，有编制好的正交拉丁方完全系或部分正交拉丁方2。

希腊拉丁方设计两个拉丁方是正交的，如果两个拉丁方有这样的性质：把一个拉丁方叠合到另一个拉丁方上时，每对字母出现且只出现一次。 为了区分两个拉丁方字母变量，习惯上以拉丁字母A，B和C表示一个拉丁方，而用希腊字母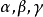 表示另一拉丁方，下面两个重叠的拉丁方被称为是一个希腊拉丁方(Graeco-Latin square)3。

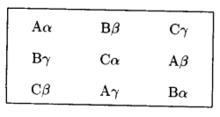
我们知道，对于素数幂k，k阶希腊拉丁方等价于k水平部分因析设计，因此，前者的构造可由后者的结构得到。阶数高于8的拉丁方和希腊拉丁方很少用到，因为难以控制大区组内的差异使得基于更高阶方的分区组效率较低3。

希腊拉丁方设计可用于处理比较，其中拉丁字母表示处理，而行、列和希腊字母表示三个分区组变量。例如考虑一个比较三种汽油添加剂的试验，试验在三辆汽车上由三个司机在三天内完成．添加剂为处理因子，分配到拉丁字母上；汽车、司机和天是分区组变量分别分配到上面的3x3希腊拉丁方中的三个行、列和希腊字母上，另外，当有两个分区组变量(由行和列表示)出现时它可用来研究由拉丁和希腊字母代表的两个处理因子。

因为其分析类似于拉丁方设计，所以下面的讨论就可以简略些。希腊拉丁方设计的线性模型是

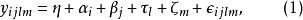其中i和j代表行和列， ，而 和m随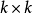 希腊拉丁方的设置变化， 是第i个行效应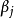， 是第j个列效应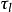， 是第l个拉丁字母的处理效应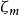， 是第m个希腊字母的处理效应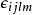， 相互独立且服从 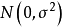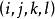， 的k2个值由集合S表示。

希腊拉丁方设计的ANOVA表总结在表1中，注意表1中的残差平方和是通过(修正)总平方和减去前四行的平方和得到的。

|| || 表1 希腊拉丁方设计的ANOVA表

超希腊拉丁方(Hyper-Graeco-Latin square)可通过叠置三个或更多个相互正交的拉丁方作为希腊拉丁方的推广而得到3。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所