[科普中国]-部分实施法

部分实施法指只挑选一部分水平组合进行实验，忽略一些高阶的交互作用效应的试验。1946年芬尼(D.J.Finney)提出了部分实施法，正交表是进行部分实施法最方便的一种工具，按正交表安排并进行分析的实验称为正交试验1。

基本介绍部分实施法指在析因试验的全部因子水平组合(处理方法)中，只挑选一部分有代表性的水平组合实施试验的方法。其优点是工作量小且结果容易控制；其缺点是试验误差较全面试验要大而估计量的精确度较小(至少理论上如此)，且试验结果的解释较复杂。

各种拉丁方设计、均匀设计、不完全区组设计、正交设计都是部分实施法的工具，其中，以正交试验设计最重要、最方便、应用也最广泛2。

析因试验设计是任意r(r≥1)个因子，每个因子取任意给定数目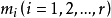水平的试验的设计；分为全面析因试验设计和部分实施析因试验设计两大类，其中因子的水平是可以控制的或者随机选取的。每个因子各取一个水平，r个水平构成一个水平组合，总共有

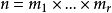个不同的的水平组合(亦称试验点或处理方法)。对每一水平组合至少进行一次试验(对—个单元进行试验)的设计叫做全面设计，其优点是能考察全部主因子效应和全部交互效应，其缺点是工作最大甚至无法实施，结果也难以控制。1946年芬尼(D.J.Finney)提出了部分实验法，即只挑选一部分有代表性的水平组合进行试验的方法，其实质是忽略全部或大部不显著交互效应(如，忽略全部三阶及三阶以上交互效应)，正交拉丁方和正交表就是部分实施的重要工具2。

相关说明与举例在有若干个因素的因子配置试验里，需要测定的次数将大为增加。而且所得到的多数资料被用于估计高次互相作用的目的，或者用于不需要十分精确的误差分析。因此，如果有5种因素或变量，分别具有两个水平的情况下，一个完整的试验就需要32次观测。这就能得出6个主要效果，一次互相作用10个，两次互相作用是10个，三次互相作用是5个，四次互相作用只有(ABCDE)1个。如果在估测时认为这些作用的任何一个都可以忽略时，则习惯上把它们看做误差的来源而被用于误差分析。

在许多情况下，与其认为高次互相作用对于保证实验精确度的良好分析值是必要的，倒不如事先假定许多高次互相作用是可以忽视的，这样则更为合理。特别是在因素中有几个大致显示出是独立变量时更是如此。如果这类的变量确实是独立的，甚至连主效应也没有的话，那么，它们的高次互相作用大概更可以忽略。通过如此处理，有时对高次互相作用作某些牺牲就能够使观测次数减少。这种方法就是人们已知的部分实施法3。

现在让我们来看一下一个最简单的例子，3个因素A、B、C各有两个水平时的情况。此时完整的试验构成下面图(1)的型式。

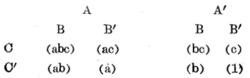
效果表现为表1的形式，其中把构成左边表示的互相作用的观测值符号列在各自的下面。 ·

|| || 表1

那么，现在假设去掉一半观测，特别是不做abc、a、b，c。此时，若再假设使用和上表同样的符号来构造剩余观测的1次组合。由于A和-BC现在已经不存在把二者区分开来的一项，所以就已经不能区分了。同样，B和-AC，C和-AB，-ABC，及总平均也不再能单独计算。因而在这种减半实施的试验里，如果可以假定BC、AC，AB的互相作用能够忽略，则可分析主要的影响。也就是说，只要进行ab、ac、bc、1的4个观测，就足以分析总平均值和三个主要影响，这时假定不存在相互作用，但是这4个观测既不提供任何检验这一假定的方法， 也不能给出分析误差的方法。

如果减半实施的个数较多，也就能得到大量的数据。若4种因素处在两个水平，则有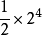即8个观测值。在可以忽略高次相互作用时，它们可用于给出4个主要影响和3个1次相互作用。假如相互作用确实能够全部忽略，则这些式中的3个就可以用于求得误差的极限值。

其他比例——譬如1/4，也是可能的。它们通常仅仅在因子个数非常多的时候才使用3。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所