[科普中国]-平均检验总数

用抽检方案(n，c)抽检不合格品率为p的多批产品，这时会出现有的批经过一次抽检就合格，而有的批则初检不合格，还需全数挑选，将这两种情况下发生的平均每批检验产品的个数称作平均检验总数，简称ATI，记为I。设交检各批的批量为N，不合格品率为p，采用(n，c)抽检方案，则平均检验总数I可由下卜式求出：I=n+(N-n)[1-L(p)]=nL(p)+N[1-L(P)]1。平均检验总数(ATI)是平均每批的总检验数目，包括样本量和不接收批的全检量，这个指标衡量了检验的经济性。

基本概念对于一定的抽样计划，为了对某一平均批质量水平做出决定，预计每批平均要检验的样品数。这种平均检验量是转移规则范围内的一个平均值，不包括拒收批中全部产品的检验。

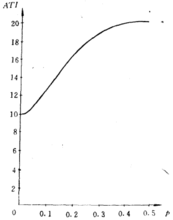
根据接收批的样本量和拒收过的批的所有产品计算出的每个批要检验的单位产品个数，称为平均检验总数(average total inspection，ATI)，这里的拒收批是要求进行100%检验的。这是评定连续生产抽样方案的经济指标之一。ATI与不合格品率p的关系见图(N=20，n=10，c=1)2。

平均检验总数的计算平均检验总数ATI因为关系到检验工作量和检验费用的大小问题，因此是设计抽样方案时应考虑的重要指标。在采用抽样检验后对接收批整批接收，对拒收批整批拒收的验收方案时，批平均检验总数就等于样本量n。但是，在采用挑选型抽样方案时，若其交验产品的批量为N，样本量为n，接收数为Ac，检验批的不合格品率为p，则对判为接收的批其检验的件数即为样本量n；而对判为拒收的批必须经过全数检验，其检验的件数为N。于是长期检验的平均检验总数ATI应为

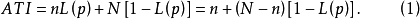由式(1)可以看出，当抽样方案确定后，平均检验总数ATI是p的函数，即。

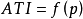同时，若p增大，ATI也增大。这是因为对于给定的抽样方案，p增大时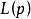，变小，即拒收的概率增加。因而，需要进行整批全检的机会增加，这就导致平均检验件数ATI也增加；此外，若N增大时，ATI也增大。这是由于当N增大时，对于拒收的批全检的件数也变大，因而平均检验总数ATI随之增大；还有，当p=0时，检验批中不存在检验批被拒收而需要全检的可能性，所以ATI值固定，且等于n3。

ATI曲线的绘制例1 设批量N=500，n=10，Ac=1的抽样方案，请画出与该抽样方案对应的平均检验总数曲线4。

解：假定一系列的批不合格批率p，利用超几何分布或二项分布的接收概率计算公式计算接收概率L(p)，然后计算合格批中的检验数nL(p)和不合格批中的检验数N(1-L(p))，得到I。

计算示例：

当p=0时，利用二项分布公式，求批接收概率。

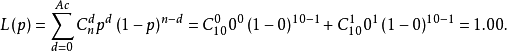
合格批的检验数是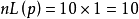

不合格批的检验数是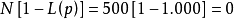

平均检验总数

当p=0.05时，利用二项分布公式，求批接收概率。

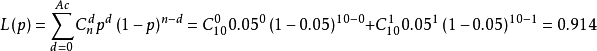
合格批的检验数是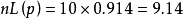

不合格批的检验数是

平均检验总数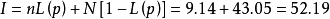

下面将假定一系列p值，并将计算结果列表如表1。

|| || 表1 平均检验总数I计算表

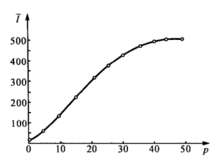
图1曲线的分析：不合格品率从0变化，当p=0时，批接收，平均检验件数ATI=n=10；随着不合格品率的增加，ATI值由于样本中的不合格品数增加，所以逐渐出现拒收批并进行全数挑选，这样ATI值出现上升趋势，直到不合格品率增到一定程度，出现所有批拒收，这样就是全检，此时ATI=N=500。所以ATI值随不合格品率的变化，它的变化范围是从n=10到N=5004。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所