[科普中国]-中心位置等距抽样

中心位置等距抽样(centrally located systematic sampling)亦称“中点定位抽样(centrically located sampling) ” 、“中点定位机械(或系统)抽样”。以被抽样总体中处在中心位置的抽样单位为起点的机械抽样。假设被抽样总体的N个单位按某种顺序排列，并依次从1到N编号，处在中心位置的：当N是奇数时为第(N+1)/2个单位，当是偶数时选第N/2或第(N+2)/2个单位。中心定位系统抽样，即取处在中心位置的单位入样，并以其为起点向两个方向上作机械抽样。可以证明，在一定条件下，这种机械抽样方法比一般机械抽样法有更高的精确度1。

基本介绍中心位置等距抽样亦称中点定位等距(系统或机械)抽样，按线性趋势排列的总体采用直线等距抽样消除偏倚的一种方法。设总体为N，按大小顺序排列，从中抽取容量为n的样本，抽样间隔为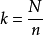，即分割为n段，每段有k个单位。当k为奇数时，取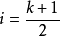；当k为偶数时取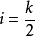或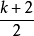作为起点，样本依次为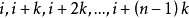，均为每一段的中点，因而可以防止偏倚。但这种方法一旦排列后，只能抽取一个固定的样本，失去了随机抽样的含义2。

等距抽样的含义等距抽样又称为机械抽样或系统抽样，它是先将总体各单位按有关标志或无关标志进行排列，再按照固定的顺序和间隔来抽选样本单位的一种抽样组织形式。

等距抽样是不重复抽样，通常可以保证被抽取的单位在总体中均匀分布，缩小各单位之间的差异程度，提高样本的代表性2。

等距抽样的方法等距抽样时，首先按照一定规则(或根据某个标志)将抽样单位依次排列，并随意确定一个抽样的“起点”，根据总体容量N和样本容量n确定抽样“间隔”——步长h=N/n；然后，以“起点”为第一个抽取的单位，并且每经h个单位抽取一个单位，依此类推。

排列方法按与调查项目无关或有关的标志排列样本，等距抽样排列方法可分为无关标志排列和有关标志排列两种。例如，按自然出现的顺序排列(如自动生产线上源源不断出现的产品、森林中的树木、交通干线上的车辆等)、按姓氏笔画排列等是无关标志排列；而家计调查按家庭收入排列、考试调查按学生的考试成绩排列等是有关标志排列。

抽选步长抽选步长(间隔)h=N/n的选取，应注意两个方面的问题：排列中可能存在某种“周期性”的变化。例如，一天24小时内高速公路某一地段的流量；商店一周内某一天的销售额等。在这种情形下，要防止步长与周期相同或为周期的倍数，否则会产生系统偏差。当h=N/n不是自然数时，应采取相应措施加以解决。例如，随机地删除一些单位，或采用首尾相连的排列方法及下面介绍的循环抽选法。

抽选方法保障样本的代表性，是等距抽样选择抽样起点的原则。常用的等距抽样法有随机起点抽样法、中点定位抽样法、对称抽样法、半步点起点抽样法、循环等距抽样法等。下面介绍抽选方法时，符号N表示总体容量，n表示样本容量，h表示抽样步长。

(1) 随机起点等距抽样法 随机起点抽样法是在依次排列的前h个单位中随机抽取一个单位入样，假设第一个入样的单位的编号为k(1≤k≤n)，那么第j(j=2,3,...,n)次抽样抽选第k+(j-1)h个单位的样本人样。需要注意的是，这种方法不宜用于抽样单位按有关标志排列的情形，因为在这种情况下可能产生系统误差。

(2)中点定位等距抽样法 在N个抽样单位排列中，选位于中点的单位做抽样起点的一种等距抽样方法。

(3)对称等距抽样法 首先依次排列在前面的h个抽样单位中，随机抽取一个做起点，假设其编号为k(1≤k≤h)；然后依次抽选第2h-k，2h+k，4h-+k，4h+k，6h-k，6h+k……个单位人样(见图1)。

(4)半步长起点等距插样法 先将总体全部N个单位的排列分为长为h的n段，抽选位于各段中点的单位入样。这种等距抽样法在实践中得到广泛应用，通常都能取得满意的结果。其局限性在于，不能严格遵循随机原则，并且无法进行样本轮换。

(5)循环等距抽样法 首先按一定规则或某个标志，将总体全部N个单位排成首尾相连的圆形，设h为最接近N/n的自然数，而k是在前h个数中任意一个自然数；以第k个单位做起点、以h为步长，一个单位一个单位地抽取直到抽够n个单位为止。

等距抽样的误差计算直接计算等距抽样的平均误差比较困难。通常是用简单随机抽样的误差公式来计算按无关标志排列的等距抽样的平均误差；用分层抽样的误差公式来计算有关标志排列的等距抽样的平均误差2。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所