[科普中国]-误差三角形

误差三角形(error triangle)是指用简化方法求最佳分向点时，当分别由三个不同边所得的三个分向点位置不能重合而组合的误差范围。简化方法可分别采用支线连接法、力多边形法、角平分线法或边线平分法等。误差范围内任意点均可视为分向点，按星形组合法进行路网规划的布局方案设计。

简介误差三角形(error triangle)是指用简化方法求最佳分向点时，当分别由三个不同边所得的三个分向点位置不能重合而组合的误差范围。简化方法可分别采用支线连接法、力多边形法、角平分线法或边线平分法等。误差范围内(图1中abc)任意点均可视为分向点，按星形组合法进行路网规划的布局方案设计1。

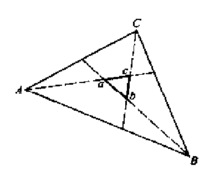
三标定位航海上，特别是沿岸航行时，最常用的是两位置线定位方法，因为它简单，迅速。但不足之处是：无法直观地判断出船位的可靠程度，既使在物标识别、铡量、标绘等方面存在粗差，也不能反映出来。在这种情况下，如一味地信赖船位，进而进行转向等一些决策，往往是十分危险的。克服二位置线定位法固有缺陷的方法便是进行三位置线定位。由于同一时刻要获得三条位置线必须要有三个以上的可观测物标，所以又叫三标定位。多于三螽以上位置线定位法，其功能与三标定位相同，因过于繁琐，故极少采用1。

三标定位法的缺点三标定位法虽能反映出定位过程的可靠性，但也有其缺点，观测次数增多，定位往往不会交于一点，而是交成一个三角形。这种三角形大小各异、成因有别，所以它们的处理方法也不尽相同。要对三角形进行正确处理，必须首先做到正确鉴别，即找出形成误差三角形的原因，不外乎有粗差，系统误差与偶然误差。粗差乃测者粗心所致，如物标识别错误、读数错误等；系统误差是指某一系统的均值，如罗经差的误差、计程仪改正率不准等引起的误差，其特点是大小固定，或能以解析式等形式确切表示2。

偶然误差偶然误差是由一些不确定的偶然因素引起，其特点是单个观测数据无规律，但许多观测数据却呈现一定的规律性，如舍人误差、绘图差等。鉴剐三角形成因及其处理方法三角形较小(通常是指在大比例尺海图上，各边不超过5毫米)时，认为主要由偶然；误差引起，处理方法是把船位取在三角形反中线的交点处。三角形较大时，应重新进行测，读、算、绘等定位过程。如果得到的新三角形仍无多大变化，则认为主要由系统误差引起。当变化较大(指边长及方向)，刚认为是偶然误差造成，刚按偶然误差处理，三角形过大(最大边长大于1.5海里)，则应考虑粗差存在的可能性3。

本词条内容贡献者为:

石季英 - 副教授 - 天津大学