正交因子模型(orthogonal factor model)是一种特殊的公共因子模型。正交因子模型的基本假设是:各个公共因子间相互独立;各个特殊因子间相互独立;各个公共因子与各个特殊因子间相互独立1。
数学模型设有p维可观测的随机向量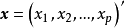 ,其均值为
,其均值为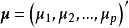 ,协方差矩阵为
,协方差矩阵为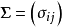 。因子分析的一般模型为
。因子分析的一般模型为
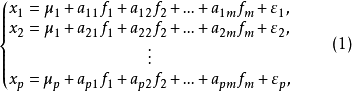
其中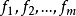 为公共因子,
为公共因子,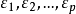 为特殊因子,它们都是不可观测的随机变量。公共因子
为特殊因子,它们都是不可观测的随机变量。公共因子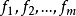 出现在每一个原始变量
出现在每一个原始变量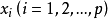 的表达式中,可理解为原始变量共同具有的公共因素;每个公共因子
的表达式中,可理解为原始变量共同具有的公共因素;每个公共因子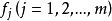 一般至少对两个原始变量有作用,否则可考虑将它归人特殊因子。每个特殊因子
一般至少对两个原始变量有作用,否则可考虑将它归人特殊因子。每个特殊因子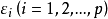 仅仅出现在与之相应的第i个原始变量
仅仅出现在与之相应的第i个原始变量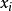 的表达式中,它只对这个原始变量有作用。(1)式可用矩阵、向量表示为
的表达式中,它只对这个原始变量有作用。(1)式可用矩阵、向量表示为
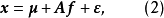 式中
式中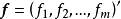 为公共因子向量,
为公共因子向量,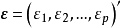 为特殊因子向量,
为特殊因子向量,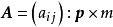 称为因子载荷矩阵。通常假定
称为因子载荷矩阵。通常假定
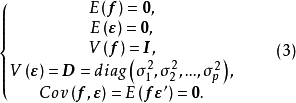 该假定和关系式(2)构成了正交因子模型。由上述假定可以看出,公共因子彼此不相关且具有单位方差,特殊因子也彼此不相关且和公共因子也不相关2。
该假定和关系式(2)构成了正交因子模型。由上述假定可以看出,公共因子彼此不相关且具有单位方差,特殊因子也彼此不相关且和公共因子也不相关2。
正交因子模型的性质1. 的协方差矩阵
的协方差矩阵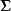 的分解
的分解
由(2)、(3)知
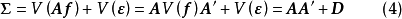
这就是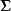 的一个分解。如果A只有少数几列,则上述分解式揭示了
的一个分解。如果A只有少数几列,则上述分解式揭示了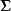 的一个简单结构。由
的一个简单结构。由
于D是对角矩阵,故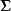 的非对角线元素可由A的元素确定,即因子载荷完全决定了原始变量
的非对角线元素可由A的元素确定,即因子载荷完全决定了原始变量
之间的协方差。如果 为各分量已标准化了的随机向量,则
为各分量已标准化了的随机向量,则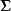 就是相关矩阵R,即有
就是相关矩阵R,即有
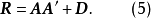
分解式(4)是在 满足正交因子模型的假定下推导出的,而对一般未作此假定的
满足正交因子模型的假定下推导出的,而对一般未作此假定的 ,(4)式是不容易准确得到的。当m=p时,任何协方差矩阵
,(4)式是不容易准确得到的。当m=p时,任何协方差矩阵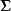 均可按(4)式进行分解,如可取
均可按(4)式进行分解,如可取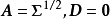 ,但此时的分解对因子分析来说是毫无意义的,因为进行因子分析的目的就是要降维。在因子分析的大多数应用中,出于降维的需要,我们希望m要比p小得多,通常只能使这种分解近似成立,近似程度越好,表明因子模型拟合得越佳2。
,但此时的分解对因子分析来说是毫无意义的,因为进行因子分析的目的就是要降维。在因子分析的大多数应用中,出于降维的需要,我们希望m要比p小得多,通常只能使这种分解近似成立,近似程度越好,表明因子模型拟合得越佳2。
2.模型不受单位的影响
将 的单位作变化,通常是作一变换
的单位作变化,通常是作一变换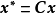 ,这里C=diag(
,这里C=diag(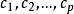 ),
),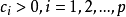 ,于是
,于是
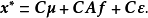 令
令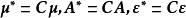 ,则有
,则有
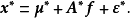 这个模型能满足完全类似于(3)式的假定,即
这个模型能满足完全类似于(3)式的假定,即
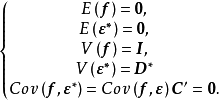 其中
其中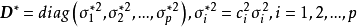 。因此,单位变换后新的模型仍为正交因子模型2。
。因此,单位变换后新的模型仍为正交因子模型2。
3.因子载荷是不唯一的
设T为任一m×m正交矩阵,令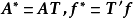 ,则模型(2)能表示为
,则模型(2)能表示为
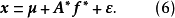 因为
因为
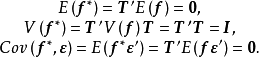 所以仍满足条件(3)。从(4)或(6)式都可看出,
所以仍满足条件(3)。从(4)或(6)式都可看出,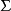 也可分解为
也可分解为
 显然,因子载荷矩阵A不是唯一的,在实际应用中常常利用这一-点,通过因子的旋转使得新的因子有更好的实际意义2。
显然,因子载荷矩阵A不是唯一的,在实际应用中常常利用这一-点,通过因子的旋转使得新的因子有更好的实际意义2。
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国