[科普中国]-稳态模型

随着控制阶层往上移动，控制信号修正的频率便会降低。在每次重新计算之前，模型运算得到的变量保持不变，直至重新计算时此变量立即成为新值，这样的模型称为稳态模型。它们有时加上一些约束条件，变化有规定的限值或变化速率有规定的限值，不能超出。这些约束可以直接表现于模型中，或对过程变量作一些限制，即使运算结果要求，也不可能继续移动。

稳态模型用于常规控制器级，经常用于求取控制器的设定值，而控制器测量值则是动态多输入计算得到的变量，如反应器生产率，分馏塔的回流量和采出速率，这些在“单元操作控制”中有所描述。

稳态模型概念和建模方法任何系统在不同的运行条件下，其运行状态都会有所不同，一般可以分为静态运行和动态运行两类。所谓静态运行，就是指系统已稳定运行在某种工作状态，其参数保持不变，系统各变量经过一定时间的调整，已经按照某一规律在有序地变化；而动态运行则是指系统运行条件或参数改变后，系统从一个稳态达到另一个稳态的过渡过程。

根据自动控制原理，在静态条件下，描述系统各变量之间关系的代数方程称为系统的静态数学模型，可用来分析系统的静态特性；而描述系统变量各阶导数之间关系的微分方程称为系统的动态数学模型，用来分析系统的动态性能。

通常，对于线性定常系统一般采用古典控制理论，建立被控对象的微分方程，然后通过拉普拉斯变换，转换为传递函数，进而在频域进行系统分析和设计。对于时变或非线性系统，因其参数随时间变化或变量是非线性的，使系统建模、分析和设计较为困难。往往采用稳态工作点附近微偏线性化方法，忽略其参数变化，建立一个近似的线性定常系统数学模型来简化处理。

在电力传动系统中，对于他励直流电动机，因电路简单且变量少，比较容易建立其数学模型；而对于交流电动机，因具有多变量、非线性和强耦合的特征，则难以建模与控制。本章以电力传动系统的稳态等效电路为基础，建立系统电压平衡方程、转矩方程和运动方程，由此建立系统的静态和动态数学模型。

对于直流调速系统，直流电动机的建模比较简单，就是直接从直流电动机的稳态等效电路出发，根据电路的基尔霍夫第一定律（KCL）和基尔霍夫第二定律（KVL），列写电动机绕组的电压平衡方程、转速和转矩方程及其运动方程。

对于交流调速系统，也是由稳态等效电路，在稳态工作点附件微偏线性化来建立其近似动态模型。由于该模型是在稳态工作点上建立的，只能描述该点的工作状态，因而称为“稳定工作点模型”或“稳态特性模型”，简称“稳态模型”。1

稳态模型的建立本次的计算忽略了泡沫的合并现象并引入下列假设：

1．系统保温良好，故忽略温度变化的影响；

2．泡沫群内气泡的形状为Kelvin（十四面体）型；

3．不考虑熔体内气体的扩散引起的泡沫行为的变化；

4．由于吹气法工艺过程的连续性，故可用稳态数学模型来描述这一过程。2

在闭孔多面体泡沫中，Plateau边界间由液膜和节点相连接。在二维情况下，泡沫群中Plateau边界的横截面面积A（x，y）、单位体积内的Plateau边界长度与体积比λ（x，y）是坐标x和y的函数，φ1=λA，φ1为液体体积分数，即含液率。在Kelvin（十四面体）型泡沫体内：

λ=5√3/(1.618×π×R2)

上式中，R气泡的等效半径。

现对任意的一条Plateau边界内的液体流动进行分析，由质量守恒定律：

а(φ1u1)/аx +а(φ1v1)/аy=0（式1）

上式中u1、v1分别是液体水平方向x和垂直方向y上的速度。Plateau边界的横截面面积采用下列公式计算：

A =（√3-π/2）×r2

上式令C=√(√3-π/2)，则A =C2r2

对泡沫析液现象的研究一般仅考虑重力和毛细管力作用下的析液过程。然而，对流动泡沫，就不得不考虑气体运动对析液的影响。二维稳态的情况下，对于任意一条Plateau边界，忽略惯性力，由力平衡原理：

Fx，毛细管力 +Fx，气体阻力 =0

Fx，毛细管力+Fy，重力+Fy，气体阻力 =U

其中，Fx，毛细管力=-Cγ/2A-1.5аA/аx，Fy，毛细管力 =-Cγ/2A-1.5аA/аy

上式中γ为熔体的表面张力。气体阻力则由以下公式计算：

Fx，气体阻力 =-150×μ×（u1-ug）/A，Fy，气体阻力 =-150×μ×（v1-vg）/A

上式中，μ表示熔体的黏度，ug和vg表示气体速度的水平分量和垂直分量，从而得到式1可转化为：2

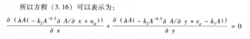
稳态模型的推导除了可以用来分析电机的瞬态行为，还可以用来得到电机的稳态模型，当电机运行在稳态时，电压、电流和磁链等变量都为正弦波。虽然通过其他方法也可以得到电机的稳态模型，而通过动态方程得到稳态模型的方法，强调了电机稳态行为只是电机动态行为的一个特例。在推导过程中，可以体会到坐标变换理论的重要作用，从而对理解稳态模型的推导过程是非常有益的。在推导前，先从物理学的角度简要地回顾一下，由正弦电压供电的感应电机具有的特性。当电机的定子绕组由对称的三相正弦电压供电时，产生定子电流和磁场。三相定子磁场相互作用，建立起在气隙中恒速旋转的合成磁场。合成磁场切割短路的转子绕组（或连接有外部回路的转子绕组），在转子中，产生感应电压，进而产生转子电流。根据Lenz 定律，感应出的转子电流阻碍磁场变化，产生的电机转矩，带动转子旋转，转子旋转的方向与合成磁场的旋转方向同向，以降低转子回路中磁链的变化率。与静止时相比，在旋转时，转子绕组中的磁链变化率变小，其中的感应电压（感应电流）的幅值和频率均变小。

现考虑正弦电压供电的感应电机，定子电压（和电流）角频率为ωe=2πfe，其中，fe是线电压频率。合成旋转磁场的电角速度为ωerad/s。假设转子的电角速度为ωrrad/s，定义一个同步旋转坐标系，定子绕组是静止的，那么其中的各变量在空间中也是静止的，频率为ωe。这些变量变换到旋转坐标系中，旋转坐标系相对于定子的旋转速度为W。转子绕组是旋转的，其中的各变量（例如：电压、电流）在空间中也是旋转的，转速为ωr，频率为ωe -ωr，这些变量变换到旋转坐标系中，旋转坐标系相对于转子的旋转速度为ωe -ωr。

可以看出，同步旋转坐标系相对于定子和转子的电角速度，分别与定子和转子变量的电角频率相同。假设定子变量和转子变量都为正弦量（频率不同），那么变换后的qd0分量则是不变的常值。因此，在正弦稳态情况下，qd0域磁链的微分为0，注意在最后得到的稳态方程中，出现了频率为ωe的阻抗。3

应用三维稳态模型的最大优点是能反映污染物传输的空间连续性，特别是垂直方向的连续性。因为它不需要进行空间离散求数值解，而是通过求解析解得到任意空问点处的污染物的浓度，这是二维动态方程办不到的（特别是求解垂直方向任意点污染物的浓度）。但由于求三维稳态方程解析解的前提是污染物浓度分布达到稳定状况，不随时间的变化而变化，因此该三维稳态模型不能反映污染物浓度的时间变化过程，这种时间上的非连续性的缺陷，使该模型不能反映受潮汐影响的水域中污染物的输运过程。

通过二维动态模型与三维稳态模型优缺点比较，两模型具有很大的互补性，即二维动态模型具有很好的时间连续性，却夸大了排污口近区的稀释作用；三维稳态模型能反映近区污染物的垂直分布规律，但不适合受潮汐影响水域所要求的时间连续性。事实上，污染物在近区和远区的输移是相互关联的。因此，可以将上述两种模型结合起来，可同时反映污染物输运的时间连续性和垂直方向的空间连续性，最终达到客观地再现污染物的迁移扩散过程。此模型的比较分析有利于完善水质模型在实际应用中的应用价值，同时为科学研究提供了科学的依据。

可以从过程设计数据，理论关系式和由过程操作或仿真得来的实验信息巾推导稳态方程或模型。从设计到理论信息推导模型，一个毛病是有时包括过多的细节因素。另一方面若单独依靠实验数据可能得不到，一些重要的关系式，这是因为在车间的工厂规模的设备上进行确定的实验有困难。在理论和实验方法间的一个很好的折衷方法是采用仿真技术建立稳态模型。4

本词条内容贡献者为:

王宁 - 副教授 - 西南大学