[科普中国]-分数问题

分数问题(fraction problem)是一种算术问题，指用分数计算来解答的应用题，它分为简单分数应用题和复合分数应用题两类。

简单的分数应用题简单的分数应用题同整数中的简单应用题类似，是最基本的分数应用题，很多较复杂的分数应用题都以它们作基础。

简单的分数应用题一般有三种形式：①求一个数是另一个数的几分之几；②求一个数的几分之几是多少；③已知一个数的几分之几是多少，求这个数。简单的分数应用题的学习，不仅可以加深对分数意义和分数乘除法意义的理解，而且还为学习较复杂的分数应用题和百分数应用题打下了基础。学习分数应用题的重点是学会分析分数应用题中的数量关系，关键是确定“标准量”，再根据分数乘除法的意义，确定解题途径和方法1。

求一个数是另一个数的几分之几这类问题是前册知识内容，为了抓住新旧知识的连接点，沟通新旧知识间的联系，构建知识网络，把新旧知识加以比较和区别，掌握各自知识的特点和内部结构，因而把“求一个数是另一个数的几分之几”这部分知识放在本册内容之前，做为新旧知识的衔接，便于进一步掌握简单应用题的三种形式的联系与区别。

分析：求一个数是另一个数的几分之几的应用题的特点是已知两个同类量，求一个量是另一个量的几分之几。解题的关键是确定标准量，把它看作单位“1”，从分数的意义出发，联系分数与除法的关系，分析题中已知条件，确定标准量，找到解答方法。

例1 某车间有职工47人，被评为先进职工的有9人，先进职工人数是全车间职工人数的几分之几?

分析：要求先进职工人数是全车间职工人数的几分之几，把全车间职工人数47人作为标准量，看作单位“1”，根据分数的意义，把47人这个单位“1”，平均分成47份，每份是1人，先进职工有9人，就占单位“1”的9份，用分数表示：先进职工人数是全车间职工人数的 。

根据分数和除法的关系，推想出计算方法： 可以看作9÷47的商，即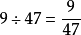 。因此，得出一个结论：求一个数是另一个数的几分之几，用一个数除以另一个数。即：比较量/标准量=几分之几。

所得的结果表示两个数的关系，不加单位名称，结果要写成分数形式。

解：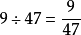

答：先进职工人数是全车间职工人数的 。

练习时可联系生活实际及学生熟悉的一些问题，以帮助学生理解和分析数量关系，防止学生死记硬背结语或公式。还可以出现求一个数是另一个数的几倍的应用题进行对比练习，使学生了解两种应用题的联系与区别。

例如：同学们去植树。五年级植树65棵，四年级植树40棵，五年级植树的棵数是四年级的几倍?四年级植树棵数是五年级的几分之几?

求一个数的几分之几是多少“求一个数的几分之几是多少”这类问题是简单的分数乘法应用题。一般的题中给出单位“1”的实际数量和所求问题的对应分率，所求问题是和单位“1”相关联的“比较量”。题目中反映出标准量、比较量和比较量对应的分率三者之间的关系，最终的目的是把比较量的对应分率。转化为实际数量。

分析：解简单的分数乘法应用题，首先要通过读题，理解题意，找出题中的关键句子，再根据分数的意义理解关键句子所表示的意义，确定单位“1”。这里的几分之几这个分率是对“一个数”来讲的，所以应该把这“一个数”作为单位”1”；“是多少”是指要求的量，即比较量的实际数量。这类题实际上就是求表示单位。1”这个实际数量的几分之几是多少。根据分数乘法的意义，用乘法来计算。

基本数量关系式是：

单位“1”的实际数量×比较量的对应分率=比较量

例2 东风小学买了100000块砖，盖房用去了 ，用去多少块砖?

分析：这道题的关键句是“盖房用去了”，这句话的意思是把买来的100000块砖看作单位“1’，把它平均分成5份，盖房用去了这样的3份，它的数量关系可以用线段图表示。

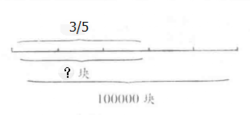
从线段图上可以看出：买了100000块砖，用去 ，求用去多少块，就是求100000块砖的 是多少。根据分数乘法的意义，求一个数的几分之几是多少，用乘法计算。

解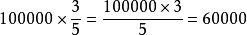： (块)

答：用去了60000块砖。

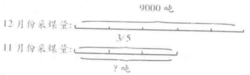
例3 某采煤队12月份采煤9000吨，11月份只是它的 。11月份采煤多少吨?

分析：根据题中“11月份的采煤量只是12月份采煤量的 ”可以得知，把12月份的采煤量9000吨看作单位“1”的量，把它平均分成5份，11月份采煤量只是这样的3份，即占单位“1”的 。要求11月份采煤多少吨，就是求9000吨的 是多少，用乘法计算。

用线段图表示：

解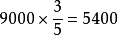： (吨)

答：11月份采煤5400吨。

已知一个数的几分之几是多少，求这个数“已知一个数的几分之几是多少，求这个数”的简单的分数除法应用题，是以后学习较复杂的分数乘除法应用题和百分数应用题的基础。它是在分数的意义、分数乘除法的意义和“求一个数的几分之几是多少”的简单的分数乘法应用题的基础上拓展的。它给出的条件是比较量的实际数量和它所对应的分率，求单位“1”的实际数量是多少。即已知部分量和它对应的分率，求整体。它的基本数量关系和“求一个数的几分之几是多少”的简单的分数乘法应用题基本相同，都是研究标准量、比较量、分率三者之间的关系。因而分析数量关系掌握分析题的方法是解题的重点。解题的关键仍然是抓住关键句子，确定单位“1”的量。

基本关系式是：

单位“1”的实际数量×比较量对应的分率=比较量

比较量÷比较量对应的分率=单位“1”的实际数量

解“已知一个数的几分之几是多少，求这个数”的简单的分数除法应用题，可以用方程解。因为它的思考方式同“求一个数的几分之几是多少”的简单的分数乘法应用题相同。运用顺向思维方法．学生比较容易掌握。计算熟练后。也可以根据分数除法的意义，用算术法解，直接用除法计算。

例4 红星农场有棉田648公亩，占耕地面积的 ，这个农场共有耕地,面积多少公亩?

分析：根据题中的已知条件“有棉田648公亩·占耕地面积的 ’’可知：把总耕地面积看作单位“1”，把它平均分成5份，棉田面积占其中的3份，即 。

如图3所示：

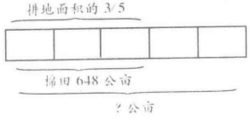
从图上可以看出：棉田面积648公亩，占这个农场耕地面积的 ，也就是，这个农场耕地面积的是648公亩。这个农场耕地面积是未知的，根据一个数乘以分数的意义，可以写出数量间相等的关系式：

这个农场耕地面积× =棉田面积

解：设这个农场共有耕地面积是 公亩。

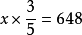
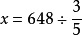
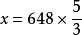
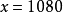
答：这个农场共有耕地面积1080公亩。

注意：方程中的结果不加单位名称1。

总结说明**(一)简单的分数乘除法应用题的数量关系及其特征。**

1．求一个数是另一个数的几分之几的应用题。

例：洗衣机厂计划生产洗衣机30000台，已经生产25000台。完成计划的几分之几?

结构特征：已知单位“1”的量和比较量，求的问题是比较量的对应分率。

数量关系：比较量÷单位。1”的量=比较量的对应分率。

解题关键：确定单位“1”的量和比较量。

解题思路：根据问题进行判断分析，确定单位“1”的量和比较量．然后用比较量的实际数量作为被除数，用单位“1”的实际数量作除数。

2．求一个数的几分之几是多少的应用题

例：洗衣机厂计划生产洗衣机30000台，已经完成了。已经完成了多少台?

结构特征：已知单位“1”的实际数量和比较量的对应分率。求的问题是比较量的实际数量。

数量关系：单位“1”的实际数量×比较量的对应分率=比较量的实际数量。

解题关键：确定单位“1”的量，找准比较量的对应分率。

解题思路：根据题目中给出的关键句，用分数的意义解释说明关键句所表示的意义，确定单位“1”的量，画出线段图，找出比较量对应的分率，根据分数乘法的意义进行判断，确定计算方法。

3．已知一个数的几分之几是多少，求这个数的应用题

例：洗衣机厂计划生产一批洗衣机，已经生产了25000台，是计划的。计划生产洗衣机多少台?

结构特点：已知比较量的实际数量和它对应的分率，所求的问题是单位“1”的实际数量。

数量关系：单位“1”的实际数量×比较量的对应分率=比较量的实际数量。或者：比较量的实际数量÷比较量的对应分率=单位“1”的实际数量。

解题思路：用分数的意义解释说明题目中关键句的意义，确定单位“1”的量，画出线段图，根据分数乘除法的意义进行判断。确定用方程解还是用算术法解1。

复合分数应用题由以上讲的三种基本应用题和其他简单应用题复合而成的问题又叫做较复杂的分数应用题。

在复合分数应用题中，既有在整数应用题中学过的数量关系，又有在分数应用题中学过的数量关系，它们混合交错出现，因此，正确判断单位“1”至关重要。

(1)含有求一个数的几分之几是多少的复合应用题。

例5 一个发电厂有煤3000吨，用去，还剩多少吨?

分析：

把原有煤的总吨数看作单位‘‘1”，根据“用去”，先求出用去的吨数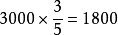：(吨)，再根据“总吨数-用去吨数=剩下吨数”2，求出还剩多少吨：3000-1800=1200(吨)。

列综合算式：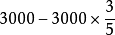

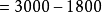
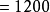(吨)

答：还剩1200吨。

(2)含有已知一个数的几分之几是多少，求原数的复合应用题

例6 修一条公路，已经修了寻，还剩12千米没修。这条公路长多少千米?

分析：

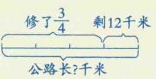
根据已知条件，应该把这条路的总长度看作单位“1”，它是未知的，不能直接用分数乘法计算，可以用方程解答。

先设这条公路长为x千米，修了，也就是修了(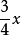)千米，因此可以列出方程：

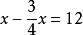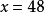，解得(千米)。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所