[科普中国]-特征根回归

当自变量之间存在线性关系时，最小二乘法回归得出的预测结果很不可靠，特征根回归(Characteristic Root Regression，CRR)是R.L.Mason和J.T.Webster等人于1974年提出的另一种改进最小二乘估计的线性有偏估计方法1。

基本介绍主成分回归仅从原自变量的样本数据中提取主成分，没有考虑自变量与因变量y的关系。作为主成分回归的推广形式，Webster等(1974)提出了特征根回归(Latent Root Regression，LRR)，将因变量也考虑进去了。同样，也是从原有数据中提取相互正交的主成分，从而在消去原自变量复共线性的同时，也使所建立的回归方程能够表征自变量与因变量之间的相关关系2。

回归系数的特征根估计假设X是由因变量y和自变量标准化处理后的数据矩阵。可以证明，由XTX的特征根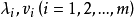可以将回归系数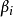的最小二乘估计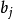表示为2

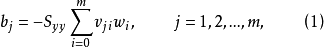式中

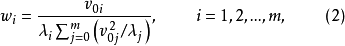
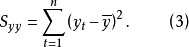
现在假设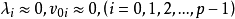。那么，就将它们略去，这样方程(1)就由剩下的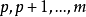项来表示，即

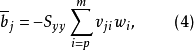式中

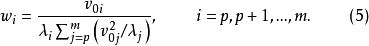
计算步骤建立特征根回归方程的计算步骤如下：

(1)对给定的因变量y和自变量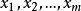进行标准化处理。将处理后的因变量放在前面，自变量放在后面，构成一个数据矩阵，记为X。

(2)计算协方差矩阵XTX，得到增广相关矩阵。

(3)求出增广相关矩阵的特征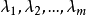及对应的特征向量。

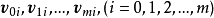(4)将同时都非常接近于0的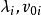去掉。在实际操作时，限定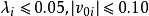就认为它们近似等于0。

(5)应用方程(4)和(5)计算回归系数的特征根估计。

(6)建立特征根回归方程2。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所