[科普中国]-方差膨胀系数

方差膨胀系数(variance inflation factor，VIF)是衡量多元线性回归模型中复 (多重)共线性严重程度的一种度量。它表示回归系数估计量的方差与假设自变量间不线性相关时方差相比的比值。

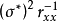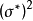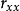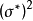基本介绍设模型已中心标准化，则回归系数估计量的协差阵为，其中是中心标准化模型误差项的方差，是自变量的相关矩阵，因此中心标准化模型的回归系数的估计量的方差等于误差项的方差和矩阵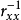中第k个对角元素的乘积。这第二个因子就称为方差膨胀系数，记为VIFk。可以证明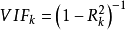，其中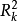是第k个自变量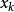与其余的自变量之间的判定系数。因此，当第k个自变量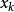与其余的自变量之间相关程度愈高，即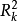愈接近1时，相应的VIFk也就越大。反之，若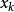与其余自变量之间相关程度很低，即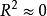时，VIFk就接近于11。

在多元回归中，我们可以通过计算方差膨胀系数VIF来检验回归模型是否存在严重的多重共线性问题。定义

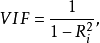
(方差膨胀系数是容忍度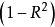的倒数。)

其中，Ri为自变量对其余自变量作回归分析的负相关系数。方差膨胀系数VIF越大，说明自变量之间存在共线性的可能性越大。一般来讲，如果方差膨胀因子超过10，则回归模型存在严重的多重共线性。又根据Hair(1995)的共线性诊断标准，当自变量的容忍度大于0.1，方差膨胀系数小于10的范围是可以接受的，表明白变量之间没有共线性问题存在2。

方差膨胀系数与多重共线性多重共线性是指自变量之间存在线性相关关系，即一个自变量可以是其他一个或几个自变量的线性组合。若存在多重共线性，计算自变量的偏回归系数时矩阵不可逆。其表现主要有：整个模型的方差分析结果与各个自变量的回归系数的检验结果不一致，专业判断有统计学意义的自变量检验结果却无意义，自变量的系数或符号与实际情况严重不符等。

检验方法主要有：容忍度(Tolerance)和方差膨胀系数(Variance inflation factor，VIF)。其中最常用的是VIF，计算公式为：

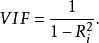VIF的取值大于1。VIF值越接近于1，多重共线性越轻，反之越重。当多重共线性严重时，应采取适当的方法进行调整3。容忍度的值界于0至1之间，当容忍度值较小时，表示此自变量与其他自变量之间存在共线性。容忍度这个变量回归系数的估计值不够稳定，则回归系数的计算值也会有很大误差。方差膨胀系数是容忍度的倒数，VIF越大，表示自变量的容忍度越小，越有共线性问题。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所