[科普中国]-交叉子样本

在抽样时，对同一个总体按照同样的抽样方法，独立或非独立地来进行两个或两个以上样本的抽取，并使得每个子样本对总体参数都提供一个有用的估计，则被抽取的子样本称为交叉子样本。交叉子样本方法最早是由印度统计学家马哈拉诺比斯(P.C.Mahalanobis，1936年)所提出，最初用于总体参数的估计，以后扩大应用于抽样和非抽样误差的估计。

基本介绍如果在随机抽样时不止抽一个样本，而是按同样的抽样方法抽取两个或两个以上的小样本，这些小样本根据研究问题的目的可以是独立地抽取，也可以不独立地抽取，这些抽取的小样本称之为交叉子样本。设是k个独立的交叉子样本对总体参数的无偏估计值，那么所有交叉子样的平均数也是的无偏估计量。即：

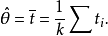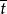而的方差为：

是估计量方差的无偏估计，计算比较简单。当k=2时，方差的公式可简化为：

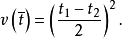这种交叉子样本的方法最初用于总体参数的估计，以后又扩大应用于估计抽样和非抽样误差等1。

在分层抽样与多阶段抽样中，要抽取容量为n的一个样 本。假定有k个调查员，则将样本随机分为k个部分——子样本，子样本容量为m=n/k。周密计划安排使每个调查员至少在两个层次或两个群类上独立随机地抽取m个抽样单位进行交叉调查，这k个容量为m的子样本，称做交叉子样本。交叉子样本主要用于确定抽样误差中， 由于调查人员的误差和回答错误所产生的，计量误差的相关部分和这部分占总误差的比例。

相关介绍交叉子样本这个方法是马哈拉诺比斯(1946年)所建议的，它对研究相关的误差特别有用。用最简单的话语来介绍，这个方法就是把一个包含n个单位的随机样本随机地划分为k个子样本，每个子样本包含m=n/k个单位。对样本的现场调查工作和数据处理工作进行了周密的计划，使各不同子样本中任何两个单位的计量误差之间没有相关。

当把交叉方法应用到包括广阔地理区域的多级样本中时，最通常的做法是采用一对对的调查员，对从逐级最小的群中抽取的交叉子样本进行计量。这样调查员被指定要调查的最终单位数仍保持调查中的习惯水平，尽管调查员必须走过的地区面积是通常地区面积的两倍。

美国普查局(1968年)曾在回答方差研究中采用这种形式的交叉方法。对1960年普查项目的总回答方差的相关分量进行了估计。这一研究中的区域是分布在整个美国的整群住户。在任何一个样本群中都有两个交叉子样本，每个子样本指定由不同的一个调查员去凋查。

交叉方法是能在分层抽样与多级抽样中推广应用的。我们确信，各不同子样本中的计量误差是相互独立的，严格地说，这就要求在各不同的子样本中采用不同的调查员，不同的监督员与不同的数据处理员。

这一方法有时称为重复抽样(replicated sampling)。戴明曾经广泛地采用过。他在1960年曾叙述过这一方法的许多应用·：对于这一方法的优点的其他讨论请见琼斯(Jones)(1955车)巧库普(1960年)的论文。采用交叉方法之后， 调查员的差旅费用增加了，但如果把样本分层为一些完整的地区，这一缺点是可以减轻的，例如，每个层可以包含两个随机样本，指派一个不同的调查员去调查，要求每个调查员在整个层中跑动，而不是只在半个层中跑动2。

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司