[科普中国]-逆预测

逆预测（Inverse prediction）也称回归控制、校准问题。当y对x的回归模型根据样本建立之后，先确定固变量y的某一取值y*，反过来去预测自变量x对应的取值x*及其区间。因这与通常的由自变量预测因变量的过程相反，故称为“逆”预测。例如在生产中往往事先规定了产品的某种标准的水平，设计或研究人员要知道相应的工艺参数(自变量值)达到什么水平，这就是逆预测问题。

基本介绍有些时候，要使用Y对X的回归模型来预测给出了新观察值Y的X的取值，这就是逆预测或统计控制。下面用两个例子来说明。

1．某贸易联合会分析人员对联合会的15个企业进行回归，研究某产品销售价格(Y)与成本(X)之间的关系，如果已知不属于这个贸易联合会的某企业的销售价格Yh(新)，要估计该企业的成本，Xh(新)。

2．以50个病例为基础进行过某种新药剂量(X)与类固醇减少水平(T)之间的回归分析。某医生正在治疗一个新病人，要求把新病人的类固醇水平降到Yh(新)，他想估计出应给病人开的新药剂量Xh(新)1。

两种情况统计控制(statistical control)(或校准)就是利用Y对Xj的回归方程，来预测给出新观察值Y的Xj的取值，这就是逆预测问题。在给定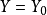 条件下，Xj估计值需分下面两种情况来考虑。

1．若Y与Xj均为随机变量，则预测和控制两问题地位是平等的。于是可把应变量看作新自变量，而把原自变量看作新应变量，重新拟合线性回归方程即可。

2．一般的控制问题，多用在自变量是非随机变量的场合(实验室、临床试验研究中多见)，因此不能像上面那样反转变量进行分析。这种情况下，预测和控制是两个性质不同的问题。控制中，X虽未知，但是一个非随机变量；而预测中，预测对象Y是随机变量2。

案例分析回归预测

如果回归直线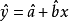经过检验，线性相关显著，就可以用它来作变量的预测。对任一给定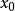的，相应的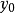一般是以回归直线上对应值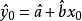为中心的服从正态分布的随机变量，设这个随机变量y的方差为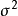，则。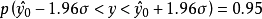

此式表明，当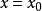时，对应y值以0.95的概率落入区间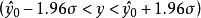，这个区间称为y的0.95预测区间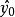，称为y的点预测值。

y的方差往往未知，但可以证明它的方差近似为

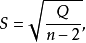其中，Q为残差平方和。

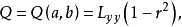所以

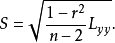
用S代替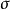，则对给定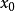概率为0.95的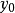预测区间为。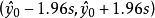

一般为方便起见，近似取1.96为2，则上述区间近似为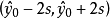，取。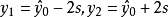

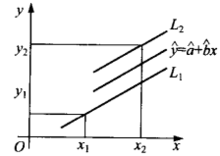
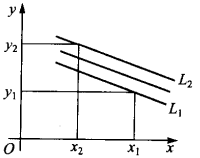
由于x值是变化的，因此y的预测区间上下限是平行于回归直线的两条直线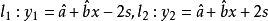，如图1(a)、(b)所示。

回归控制

如果希望y落在区间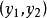内，则x取值区间可由图1中直线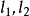对应关系确定。
设

解出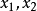，则

当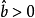时，控制区间为；

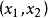当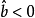时，控制区间为。

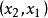但必须注意，只有当时，所求控制区间才有意义3。

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司