[科普中国]-完全信息最大似然法-

完全信息最大似然法(FIMI)是一种完全的系统方法，此方法考虑所有的结构方程提供的信息，也就是说，这种方法应用于结构模型中的所有方程式，然后利用最大似然法同时估计出所有结构参数的估计值。此方法的估计量具有一致性和渐进有效性。这种方法的优点是在估计过程中充分利用了模型中提供的信息，但计算量很大，即使利用计算机，也会感到工作量很大。除了相当小的模型外，在许多情况下可能遇到自由度的困难。因此，这是一种不寻常的联立方程估计方法1。

基本介绍在最小二乘估计技术族中，既有单一方程估计法，像直接与间接的最小二乘法、二阶段最小二乘法和最小方差比估计法，又有系统估计法，即利用整个系统经济模型的结构性质并同时对所有的结构参数进行估计的方法，如三阶段最小二乘法。类似地，在最大似然估计技术族中，有单一方程估计法(如有限信息最大似然法)，也会有系统估计法。这种系统估计法被人们称为完全信息****最大似然法(Full Information Maximum Likelihood Estimator，简称FIML)2。

完全信息最大似然法指在同时考虑所有结构方程的约束的前提下，用最大似然法估计结构方程的参数。完全信息最大似然法是一种系统估计方法，它适用于过度识别的方程系统。这种方法是先求扰动项的似然函数，然后根据关于扰动项的似然函数导出关于内生变量的似然函数。最后求似然函数在所有约束条件下的极大似然值3。

FIML法的假设1. FIML法要求使用完全信息，即要求对整个模型是完全了解的，不但需要知道在模型中出现的所有内生变量和所有前定变量，而且需要知道每个方程式的数学形式。这就必须正确设定所有结构方程式。

2. 要求每个结构方程式都是可识别的(恒等式除外)，特别允许是过度识别的。如果模型中有某些结构方程式不能识别，那么该模型必须重新设定。

3. 每个结构方程式的随机扰动项要求满足通常的假定：零平均值，同方差，序列无关，遵从正态分布4。

FIML法和LIML法的比较FIML法和LIML法的比较：

相同点：

(1)它们都是从ML法发展改进而来的。

(2)它们都适合于过度识别的结构方程式。

(3)它们所求得的参数的估计量都具有一致性特性。

相异点：

(1)LIML法是单一方程方法，FIML是方程组方法。

(2)LIML法只使用了“有限信息”，而FIML法使用了“完全信息”，在这种意义上，FIML法比LIML法更为有效。

(3)FIML法比LIML法计算过程复杂，要花费更多的时间和付出更多的成本。

关于FIML的几点说明1. 当方程组模型是递归式时，由于雅可比行列式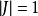，那么完全信息极大似然估计量所满足的方程组对估计量是线性的。在这样的情况下较易于求解。

2. FIML法要求对整个联立方程组模型都要正确设定。与其它方法相比较对设定误差更为敏感。

3. 由于要同时求出模型中所有参数的估计量，因此要求样本容量足够大。又由于在求解估计量时，涉及关于参数的非线性方程组，这是较为困难的工作。因此，FIML法在实际工作中还没有被普遍使用4。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所