[科普中国]-限制容量分配模型

限制容量分配模型是指在交通量分配时，考虑随着路段交通量的增加，受路段通行能力的限制，车辆行驶速度逐渐降低，路段通过时间增加，后续分配的交通量重新选择新的“最短路径”进行分配的模型，它是交通规划的重要组成部分，是研究交通流量均衡、路网结构、道路建设等的基础。1

简介容量限制分配是一种动态的交通分配方法，它考虑了路权与交通负荷之间的关系，比较符合实际情况。采用该方法分配出行量时，需先将原O-D表（n×n）阶分解成K个O-D分表（n×n）阶，然后分K次用最短路分配模型分配O-D量，每次分配一个O-D分表，并且每分配一次，采用路阻函数修正一次路权，直到把k个O-D分表全部分配到网络上。

原理该法有容量限制-增量加载分配和容量限制-迭代平配两种形式。前者先将原OD表分解成K个分表，再进行K次最短路径的分配。每分配一次，需按路阻函数修正一次出行时间，或修正以其他定量值表示(如成本)的阻抗，直至K个OD分表全部分配完毕。分配次数K和每次分配的OD量比例视道路网络的大小而定。一般取K=5，每次分配量分别为30%、25%、20%、15%、10%。后者不需分解OD表，先假设各路段交通量为零，据此计算阻抗，用最短路径法进行分配，然后再按分配上去的交通量计算新的阻抗，再分配新的交通量，比较前后两次的阻抗和交通量，若满足精度要求则停止迭代，否则继续迭代，直至达到精度。由于能事先估计工作量，便于上机安排，后者比前者应用更多。

容量限制下的交通分配交通分配是交通规划的重要组成部分，是研究交通流量均衡、路网结构、道路建设等的基础。交通分配的理论研究及仿真模拟表明，随机用户平衡（SUE —Stochastic User Equilibrium）分配比确定性用户平衡（UE —User Equilibrium）分配及系统最优（SO —System Optimization）的分配更具有合理性，在容量限制条件下的交通分配是一种混合的交通，即存在系统最优信息下的分配，也存在用户的随机决策。

随着经济的发展，交通需求日益提高，不可回避的要出现交通拥挤的情形，该情形不是简单的经济上所谓需求与供给的平衡，而是受制于交通规划影响的结果，它是一个完全信息下的Stackelberg博弈均衡。由于供给受经济水平和土地使用等制约，特别是在城市道路交通中，路网交通容量瓶颈一直是交通规划的研究重点。交通容量取决于路段容量和路网容量，而路网容量最终取决于路段容量，二者之间的关系密切但复杂，不能简单的用“正比例”来描述。研究容量限制要从路段的阻抗入手，根据分配手法可分为路段阻抗可变和阻抗不变两类，前者多用于传统交通规划;后者能较好的反映路段的交通流的实际状况，因此它成为解决容量限制的交通规划所常采用的方法。2

模型改进及软件开发改进不少学者针对我国的交通实际情况，试图用行驶时间与机动车、非机动车交通负荷之间的线性或非线性回归关系式作为路阻函数。原则上这种路阻函数考虑了机动车、非机动车交通负荷的影响，比较符合实际情况。但通过研究发现，采用这种方法确定的回归关系式相关系数很低，远远不能满足工程设计要求。可见采用简单的回归经验公式作为路阻函数是不合理的，缺乏理论依据，且通用性受到很大限制。而纯理论的路阻函数不能反映实际的交通状况，故采用半理论半经验的路阻函数比较合理。即先根据流量、车速、密度三参数关系确定路阻函数的理论模型理论模型中只考虑机动车交通负荷的影响，然后对理论模型进行非机动车交通负荷、车道数、车道宽度等影响修正。3

软件开发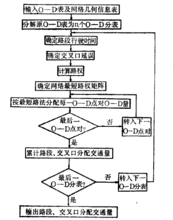对于容量限制分配，采用先进的true basic语言编制软件编制，执行框如右图所示。该软件有速度快、通用性强的特点，适用于大中城市的交通规划。

优势由于容量限制交通分配模型具有快速、省内存等优点而被广泛采用。改进后的容量限制分配模型，保留了原模型的结构，其主要内容全部被更新或充实，使模型更加完善，特别适用于我国的城市交通规划及区域公路网规划。

本词条内容贡献者为:

宋春霖 - 副教授 - 江南大学