[科普中国]-非退化矩阵

非退化矩阵(non-degenerate matrix)又称“非异矩阵(non-singular matrix) ”、“满秩矩阵”，若n阶矩阵A的行列式|A|≠0，则称A为一个非退****化矩阵，若|A|=0，则称A为“退化矩阵”，也称“奇异矩阵”、“降秩矩阵”。n阶方阵A是非退化的充要条件为A是可逆矩阵1。

基本介绍先引进逆矩阵的概念。

对给定的矩阵A，如果存在矩阵B，使成立

则称A为非退化(矩)阵(non-degenerate matrix)，并称适合式(1)的矩阵B为A的逆(矩)阵(inverse matrix)；非退化阵也称可逆阵(invertible matrix)或非奇异阵(non-singular matrix)。

可以看出，只有方阵才可能有逆矩阵，而且可以证明，对方阵A，B，若AB=I，则必BA=I，故今后在讨论方阵时，只要成立AB=I或BA=I就可以说明A，B互为逆阵了2。

相关结论定理 如果A是非退化阵，则其逆阵是惟一的。

证： 可用同一法证明结论。设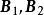是对非退化阵A的适合式(1)的任意两个矩阵，则必有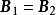。事实上，根据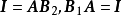以及下文式(2)，有

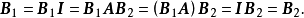证毕。

在证明过程中巧用式(2)以及式(1)的做法，称之为单位阵技巧，这是在证明矩阵等式中时常有用的一种技巧，

由于可逆阵A的逆阵为惟一确定，故可记之为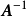，有

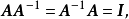而称不存在逆阵的方阵为退化(矩)阵(degenerate matrix)2。

这样，由逆阵概念可容易地推知，单位阵必为非退化阵，且其逆阵即为自身，即有

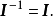
定理 对m×n矩阵A，有

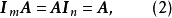以及对适当维的零矩阵，总有

及.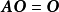

在有可能用上这些明显等式时，能简化矩阵乘法的运算过程。

由于矩阵乘法是满足结合律的，在一个方阵自乘若干次的情形，使用幂指数的记号是既合理又可带来便利的。若k是个自然数，定义(规定)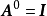

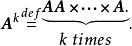从这个定义可以看出成立指数律：

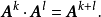
结论 一个n×n矩阵是非退化的充要条件是它的秩等于n。

推论 设A，B都是数域F上的n×n矩阵，矩阵AB为退化的充要条件是A，B中至少有一个是退化的。

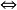
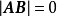
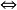
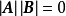
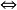
证明 AB为退化学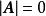或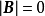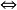A退化或B退化3。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所