[科普中国]-帽子矩阵

帽子矩阵(hat matrix)是指一类正交投影矩阵。对帽子矩阵又叫帽变换或K-T变换。

对于线性模型Y=Xβ+e，E(e)=0，cov(e)=σ2I，矩阵H≙...X（XTX）-1XT是将观测向量Y正交投影到由X的列向量所生成的子空间上的投影矩阵。Y^=HY，习惯上称H为帽子矩阵。

简介帽子矩阵(hat matrix)是指一类正交投影矩阵。对帽子矩阵又叫帽变换又叫K-T变换。对于线性模型Y=Xβ+e，E(e)=0，cov(e)=σ2I，矩阵H≙...X（XTX）-1XT是将观测向量Y正交投影到由X的列向量所生成的子空间上的投影矩阵。Y^=HY.习惯上称H为帽子矩阵1。

帽子矩阵的性质帽子矩阵的性质如下图所示2：

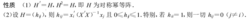
帽子矩阵的作用帽子矩阵在回归诊断，残差分析中有着特殊的作用，讨论帽子矩阵H=(hij)元素性质非常重要3。

矩阵在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。

矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；计算机科学中，三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。关于矩阵相关理论的发展和应用，请参考矩阵理论。在天体物理、量子力学等领域，也会出现无穷维的矩阵，是矩阵的一种推广2。

矩阵的历史矩阵的研究历史悠久，拉丁方阵和幻方在史前年代已有人研究。

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。作为解决线性方程的工具，矩阵也有不短的历史。成书最迟在东汉前期的《九章算术》中，用分离系数法表示线性方程组，得到了其增广矩阵。在消元过程中，使用的把某行乘以某一非零实数、从某行中减去另一行等运算技巧，相当于矩阵的初等变换。但那时并没有现今理解的矩阵概念，虽然它与现有的矩阵形式上相同，但在当时只是作 为线性方程组的标准表示与处理方式。

矩阵正式作为数学中的研究对象出现，则是在行列式的研究发展起来后。逻辑上，矩阵的概念先于行列式，但在实际的历史上则恰好相反。日本数学家关孝和（1683年）与微积分的发现者之一戈特弗里德·威廉·莱布尼茨（1693年）近乎同时地独立建立了行列式论。其后行列式作为解线性方程组的工具逐步发展。1750年，加布里尔·克拉默发现了克莱姆法则2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学