拉格朗日密度即拉格朗日量,实质为从粒子体系推广到场体系的自然对应。
在分析力学里,一个动力系统的拉格朗日量(英语:Lagrangian),又称为拉格朗日函数,是描述整个物理系统的动力状态的函数,对于一般经典物理系统,通常定义为动能减去势能。
在分析力学里,假设已知一个系统的拉格朗日量,则可以将拉格朗日量直接代入拉格朗日方程,稍加运算,即可求得此系统的运动方程。
拉格朗日量是因数学家和天文学家约瑟夫·拉格朗日而命名。
概念拉格朗日量是动能T与势能V的差值:
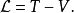 通常,动能的参数为广义速度
通常,动能的参数为广义速度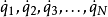 (符号上方的点号表示对于时间{\displaystyle t}的全导数),而势能的参数为广义坐标
(符号上方的点号表示对于时间{\displaystyle t}的全导数),而势能的参数为广义坐标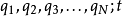 ,所以,拉格朗日量的参数为
,所以,拉格朗日量的参数为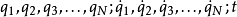 。解析一个问题,最先要选择一个合适的广义坐标。然后,计算出其拉格朗日量。假定这些参数(广义坐标、广义速度)都互相独立,就可以用拉格朗日方程来求得系统的运动方程。
。解析一个问题,最先要选择一个合适的广义坐标。然后,计算出其拉格朗日量。假定这些参数(广义坐标、广义速度)都互相独立,就可以用拉格朗日方程来求得系统的运动方程。
假设一个物理系统的拉格朗日量为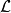 ,则此物理系统的运动,以拉格朗日方程表示为
,则此物理系统的运动,以拉格朗日方程表示为
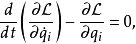 其中,
其中,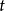 是时间,
是时间,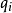 是广义坐标,
是广义坐标,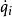 是广义速度。
是广义速度。
拉格朗日量与作用量的关系一个物理系统的作用量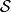 是一种泛函,以数学方程定义为
是一种泛函,以数学方程定义为
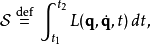 其中,
其中,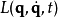 是系统的拉格朗日量,广义坐标
是系统的拉格朗日量,广义坐标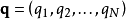 是时间
是时间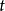 的函数,
的函数,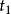 和
和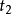 分别为初始时间和终结时间。
分别为初始时间和终结时间。
假若,作用量的一次变分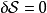 ,作用量
,作用量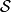 为平稳值,则
为平稳值,则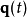 正确地描述这物理系统的真实演化。从这变分运算,可以推导出拉格朗日方程
正确地描述这物理系统的真实演化。从这变分运算,可以推导出拉格朗日方程
详尽相关导引,请参阅拉格朗日方程。1
拉格朗日表述重要性拉格朗日表述是经典力学的一种重新表述。拉格朗日表述的重要性,不只是因为它可以广泛应用在经典力学;而更是因为它能够帮助物理学家更深刻地了解一个物理系统的物理行为。虽然拉格朗日只是在寻找一种表述经典力学的方法,他用来推导拉格朗日方程的平稳作用量原理,现在已被学术界公认为在量子力学也极具功用。
优点拉格朗日表述不会被任何坐标系统捆绑住。拉格朗日表述使用广义坐标来描述系统的空间参数。它所涉及的物理量是动能与势能,这些物理量的值不会随广义坐标的选择而改变。因此,对于系统的种种约束,可以选择一组最合适的广义坐标,来计算问题的解答。
拉格朗日表述能够简易地延伸至其他学术领域。电路学、量子力学、粒子物理学、等等,都可以用拉格朗日表述来分析。
如果用同样的表述可以分析不同学术领域的物理系统,这些系统必定有结构上的类推。在一个学术领域的新发现,意味着很可能在另一个学术领域会有类似的现象。
可略坐标和守恒定律拉格朗日量有一个优良的性质,那就是守恒定律可以很容易地从它的表达式读出来。例如,假设拉格朗日量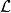 跟某广义速度
跟某广义速度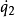 有关,而跟广义坐标
有关,而跟广义坐标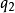 无关,则对应的广义动量
无关,则对应的广义动量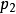 是一个守恒量。这种坐标称为“可略坐标”,或“循环坐标”。更详细地说,拉格朗日量的形式为
是一个守恒量。这种坐标称为“可略坐标”,或“循环坐标”。更详细地说,拉格朗日量的形式为
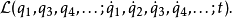
直接检视,就可以发觉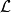 跟
跟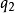 无关,因此可以推断
无关,因此可以推断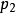 是一个守恒量。
是一个守恒量。
以此类推,假设,时间 不在
不在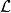 的表达式里面,则哈密顿量守恒,即能量守恒。这种物理行为是诺特定理的一个特别案例。1
的表达式里面,则哈密顿量守恒,即能量守恒。这种物理行为是诺特定理的一个特别案例。1
检验粒子的拉格朗日量假定检验粒子的质量和电荷超小,其对于外在系统的影响可以忽略。检验粒子时常可以想像为简单的质点粒子,只拥有质量和电荷性质。像电子或上夸克一类的真实粒子具有更复杂的性质,它们的拉格朗日量含有更多项目。
狭义相对论里的拉格朗日量在狭义相对论的四维空间里,一个移动中的粒子的相对论性拉格朗日量可以写为
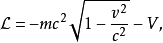 其中,m是粒子的静质量,c是光速,v是粒子的速度。
其中,m是粒子的静质量,c是光速,v是粒子的速度。
其拉格朗日方程为
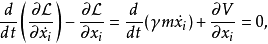 其中,
其中,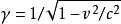 是洛伦兹因子。
是洛伦兹因子。
注意到动量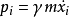 、作用力
、作用力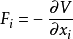 。将这些公式代入拉格朗日方程,就可复制牛顿第二定律的方程:
。将这些公式代入拉格朗日方程,就可复制牛顿第二定律的方程:
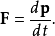
因此,这拉格朗日量被认定为正确无误。
这粒子的广义动量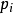 定义为
定义为
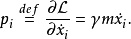
假设这物理系统的势能为零,这粒子是自由粒子,则此系统的能量函数h为
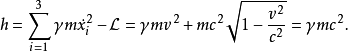 这是质能方程:粒子的总能量等于其质量乘以光速平方。
这是质能方程:粒子的总能量等于其质量乘以光速平方。
假设粒子速度超小于光速,则拉格朗日量的动能部分可以近似为
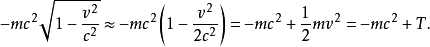 静质量的能量
静质量的能量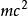 是个常数,可以忽略(其变分等于零)。相对论性拉格朗日量又变回经典拉格朗日量:
是个常数,可以忽略(其变分等于零)。相对论性拉格朗日量又变回经典拉格朗日量:
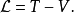
参见哈密顿量
哈密顿原理
拉格朗日力学
哈密顿力学
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国