[科普中国]-湍流剪应力

湍流剪应力又可称为湍流切应力。流体作湍流运动时所产生的应力，除了粘性应力外尚有附加的应力，包括法向附加应力和切向附加应力，这些附加的应力都是湍流所特有的。所以湍流应力可以分为切应力和正应力，而其中切应力又可以分为雷诺切应力和黏性切应力两部分。

基本概念在湍流中，一方面因时均流速不同，各流层间的相对运动仍然存在粘性切应力，粘性切应力可由牛顿内摩擦定律求出。另一方面，由于湍流质点存在脉动，相邻流层之间有质量的交换。低速流层的质点由于横向运动进入高速流层后，对高速流层起阻滞作用；反之，高速流层的质点在进入低速流层后，对低速流层却起推动作用。也就是由质量交换形成了动量交换，从而在流层分界面上产生了湍流附加切应力。

公式推导用动量方程来推导湍流附加切应力 。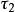

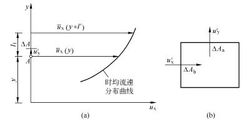
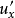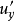如图1所示，在空间点A处，具有x和y方向的脉动流速 和 。在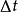 时段内，通过 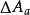的脉动质量为：

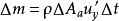
这部分流体质量，在脉动分速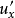 的作用下，在流动方向的动量增量为：

此动量等于湍流附加切力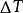 的冲量，即：

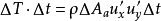
因此，附加切应力为：

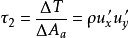
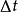现取时均值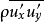 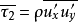， 就是单位时间内通过单位面积的脉动微团进行动量交换的平均值。取基元体（如图1（b）），以分析纵向脉动速度 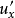与横向脉动速度 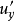的关系。根据连续性原理，若时段内，A点处微小空间有 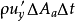质量自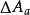 面流出，则必有 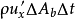的质量自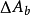 面流入，即：

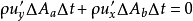
则

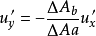
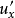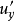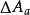由上式可见，纵向脉动流速 与横向脉动速度 成比例，而 与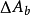 总为正值。因此 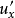与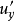 符号相反。为使附加切应力 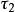以正值出现，在式 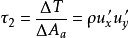中加一负号，得：

上式就是用脉动流速表示的湍流附加切应力基本表达式。它表明附加切应力与粘性切应力不同，它与流体粘性无直接关系，只与流体密度和脉动强弱有关，是由微团惯性引起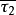， 又称为惯性切应力，是雷诺于1895 年首先提出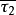， 也可称为雷诺应力。

在湍流流态下，湍流切应力为粘性切应力与附加切应力之和，即：

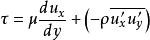
两部分切应力的大小随流动情况而有所不同。在雷诺数较小，脉动较弱时，前项占主要地位。随着雷诺数增加，脉动程度加剧，后项逐渐加大。到雷诺数很大，紊动已充分发展的湍流中，前项与后项相比甚小，前项可以忽略不计。

混合长度理论然而脉动速度瞬息万变，由于对湍流机理还未彻底了解，式 不便于直接运用。主要采用半经验的方法，即一方面对湍流进行一定的机理分析，另一方面还得依靠一些具体的实验结果来建立附加切应力和时均流速的关系。湍流的半经验理论是工程中主要采用的方法。虽然各家理论出发点不同，但得到的湍流切应力与时均流速的关系式却基本一致。1925 年德国学者普朗特(L.Prandtle)提出的混合长度理论，就是经典的半经验理论。

普朗特设想流体质点的湍流运动与气体分子运动类似。气体分子走完一个平均自动路程才与其他分子碰撞，同时发生动量交换。普朗特认为流体质点从某流速的流层因脉动进入另一个流速的流层时，也要运行一段与时均流速垂直的距离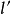 后才和周围质点发生动量交换。在运行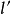距离之内，微团保持其本来的流动特征不变。普朗特称此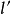为混合长度。如空间点A处(图1(a))质点A沿x方向的时均流速为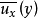，距A点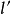处质点x方向的时均流速为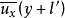，这两个空间点上质点沿 x 方向的时均流速差为：

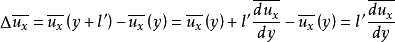
普朗特假设脉动速度与时均流速梯度成比例，为了简便，时均值不再标以时均符号，即：

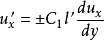
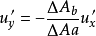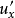从式可知与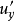具有相同数量级，但符号相反，即：

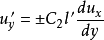
于是：

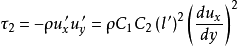
略去下标x，并令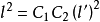，得到湍流附加切应力的表达式为：

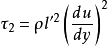
混合长度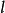是未知的，要根据具体问题作出新的假定结合实验结果才能确定。普朗特关于混合长度的假设有其局限性，但在一些湍流流动中应用普朗特半经验理论所获得的结果与实践能较好符合，所以仍然是工程上应用最广的湍流理论。1

本词条内容贡献者为:

陈红 - 副教授 - 西南大学