[科普中国]-一阶形式语言

所谓一阶(形式)语言，就是用狭义谓词演算范围内的逻辑概念所表达的语言，具体地说，就是用个体变元、个体常元、函数符号、关系符号或称谓词符号（一般包括等号在内），以及与、或、非、蕴涵等命题连接词，还有“存在一个体”和“对一切个体”两种量词所表达的语言。其特点是，量词“存在”、“对一切”只允许对个体使用，不允许对集合或谓词等使用。它不包括“存在（个体集合的）一个子集”这样的量词。一阶模型论的语言是一阶语言。在一阶语言中，由任一组命题所成的集合T称为一个形式理论。如果有一个数学结构M，当用其中的概念解释T的命题中诸符号后，能使T的每一命题都在M中成立，则称M是T的一个模型。一阶逻辑的模型论是模型论的基础，事实上，任何一种逻辑系统都有各自的模型论。除各种逻辑的模型论外，模型论的新发展层出不穷：用模型论手法来研究逻辑系统也叫做模型论逻辑；用模型论方法比较各种逻辑系统的强弱，分析各种逻辑系统的特点，叫抽象逻辑的模型论；用递归论方法研究模型论问题产生递归模型论；只研究有限模型的构造和判定叫有限模型论；用模型论的思想去研究代数结构、群、环、模、域等叫做代数模型论；研究模型分类的理论叫稳定性理论。现代模型论对计算机科学也有一定影响1。

基本介绍一阶形式语言由以下部分构成。

(1)字符表

个体变元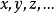：，或者。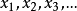

常元：。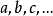

函数符号：。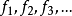

谓词符号：。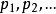

特殊谓词符号：=。

逻辑联结词：。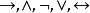

量词：。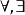

括号：(，)。

(2)形成规则

①项的形成规则：

(i) 任一个体变元，任一常项变元c都是一个项。

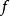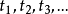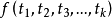(ii) 若是一个带k个自变元的函词，是项，则是一个项。

(iii)只有由定义(i)~(ii)归纳定义得到的字符串是项。

②公式的形成规则：

(i)若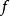是一个带k个自变元的函词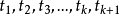，是项，则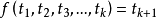是一个公式。

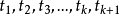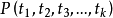(ii)若p是一个带k个自变元的谓词，是项，则是一个公式。

(iii)若A，B是公式，则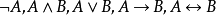是公式。

(iv)若A是公式，是一个变元，则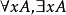是公式。

(v)只有由(i)~(iv)归纳定义得到的字符串是公式。

(3)语句形成规则

如果公式A不含任何自由变元，则是A语句。上述结构构成一阶语言。

(4)给定一阶语言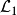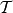，是一个一阶理论，如果它包括：

①谓词演算的所有公理；

②一个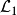中语句组成的集合，有穷或者无穷，它们构成非逻辑公理；

③谓词演算的所有推理规则。

(5)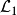中的一个语句A是理论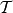的一个定理，如果A是(4)中的①或②语句，或者是以逻辑公理或非逻辑公理为前提，使用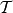的推理规则得到的语句。

(6)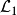中的一个结构(或称模型)M由一个论域D及一阶公式的变元的解释V所组成的非空集合构成，记作：

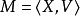对于项；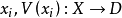

对于函词；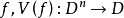

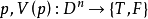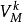对于谓词，用或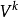表示V的某一次(个)映射，如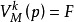表示V的第k次(个)映射使p为假。

一阶形式语言的研究有时被称为一阶逻辑，或者初等逻辑。它构成现代逻辑的大部分内容。但是，现代逻辑的奠基者如弗雷格、皮亚诺以及怀特海和罗素等人都提出过高阶语言的问题。

高阶逻辑比一阶逻辑有更强的表达力。一阶逻辑的“局限性定理”表明一阶语言在表达资源上的限制。诸如有限性、可数性和良基性等许多中心数学概念都不能在任何一个一阶语言中得到表达，自然数集、实数域以及欧几里得空间等结构也都不能得到充分的描述。这些局限性定理没有一个适用于高阶语言，而且上述概念和结构也都有二阶刻画。二阶和高阶语言因此也有很强的表达力，几乎和非形式的数学语言一样强。结果，它们更难以研究，也更难以驾驭。

一阶形式语言是目前应用最普遍的逻辑语言。但是，一阶形式语言的语法生成能力有一定的局限性。它没有部分量词。在改进后即增加部分量词符号和量词运算功能后，它可以方便地表示亚里士多德三段论的改进形式：扩展的三段论(如果认为亚里士多德三段论包括部分量词命题的话，也需要一阶形式语言的改进)。

相关概念一阶形式语言相关重要概念定义如下：

一阶命题变元的解释是对(项或谓词或函词)变元的一个赋值(实例化)。

有量词约束的公式称为量化公式。

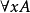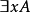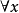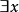对一个量化公式(或)，称其子公式A是量词(或)的辖域。

在公式A中，一个变项如果出现在某个形如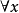(或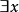)的量词的辖域中，或它就紧跟在∀(或∃)后面，则称在A中的这处出现是约束的。变项的非约束的出现，称为自由出现。

如果在A中有一处自由出现，则称是A中的自由变项。如果在A中的所有出现都是约束的，则是A中的约束变项。

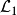是形式化的，也是语法化的，即按照这些符号和句法规则可以或接近构成或验证一个一阶语言的证明系统2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学