解释性证明方法是同构证明方法的特例,令P是命题集合,或其定义域,或参数测试样例的集合,PI是它的映射(另外的命题集合及其定义域或参数测试样例), PG是P的推论,如果存在PG与 PI同构,则称P具有I-解释性证明,即G(P→PI)=PG→(PI)G是解释性证明,其中,G是同构算符。
基本介绍考虑一个由公理构成的证明系统P,可以将P转换为Q。这种转换可能有多种目的,例如:
(1)P的公理不完全被另一个系统Q接受,需要建立P和Q公理的对应关系;
(2)P公理的域与Q的域并不相同(例如,自然数与超穷数的差别),需要转换后才有效;
(3)P公理经过转换后更有利于证明,等等。
这样,这种转换也称为解释,它既包含P公理的转换,即P公理解释为Q公理,也可以对P公理的定义域进行解释,以验证P公理的有效性1。
定义1令P是命题集合,或其定义域,或参数测试样例的集合,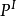 是它的映射(另外的命题集合及其定义域或参数测试样例),
是它的映射(另外的命题集合及其定义域或参数测试样例), 是P的推论,如果存在
是P的推论,如果存在 与
与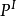 同构,则称P具有
同构,则称P具有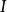 -解释性证明,即
-解释性证明,即
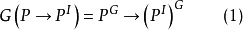 是解释性证明,其中,G是同构算符。
是解释性证明,其中,G是同构算符。
式(1)如图1所示。
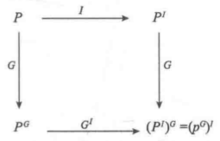
可见解释性证明是同构性证明(参见“同构证明方法”)的一种特例,它多伴有输入自变元的调整变化作为附加条件。一个解释性证明的实例是哥德尔对PA证明的功能解释。另外的一种实例是归结方法,它是通过自变元的反例输入证明原命题的否定的不可证证明原命题。
当式(1)中的P不是命题,而是自变元,这时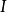 解释P为
解释P为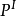 ,从而
,从而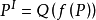 ,其中Q是命题,这样可以通过计算性的方法得到
,其中Q是命题,这样可以通过计算性的方法得到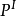 ,并使
,并使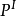 成为独立的“模块”被其他证明所调用,也可以采用不同的算法得到不同的解释。这种方法即构成“证明挖掘”(Proof Mining),或者“开放式证明”(Unwinding Proof)。这两种称呼,前者起源于G Kreisel,后者起源于D.Scott。
成为独立的“模块”被其他证明所调用,也可以采用不同的算法得到不同的解释。这种方法即构成“证明挖掘”(Proof Mining),或者“开放式证明”(Unwinding Proof)。这两种称呼,前者起源于G Kreisel,后者起源于D.Scott。
相关概念同态与同构设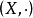 和
和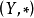 是两个同类型的代数系统(代数系统是集合及其运算构成的系统),
是两个同类型的代数系统(代数系统是集合及其运算构成的系统),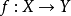 是一个映射,如果对于任意元
是一个映射,如果对于任意元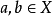 恒有
恒有
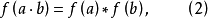 则称
则称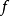 是
是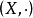 到
到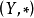 的一个同态映射,并称
的一个同态映射,并称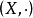 和
和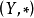 同态,用
同态,用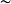 表示;如果
表示;如果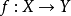 是一个双射,则称
是一个双射,则称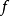 是
是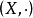 到
到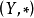 的一个同构映射,
的一个同构映射,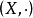 与
与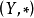 同构,用
同构,用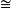 表示。
表示。
同态和同构是布尔巴基学派提出的重要概念,它是对于结构之间关系的描述。虽然同构概念提出较晚,但其意义是极其深远的。同构不仅是数学的证明方法,也是基本的心理结构和人类思维的基本方式1。
同构性证明在证明中对如式(3)、式(4)、式(5)任意一命题的运用是同构证明方法:
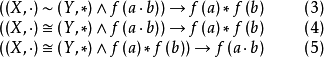
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国