对于一个以 A 为顶点集的抽象复形 ?,复形 ? 中的元素称为复形 ? 的抽象单形。
简介引入抽象复形是几何复形的一种抽象,将几何单纯复形的一些良好性质,利用同构复形的思想,加以抽象化就得到抽象复形的概念。同构的复形对应同一个抽象复形。
设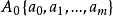 是非空的有限几何,? 是 A 中某些指定的非空子集组成的子集族,称 ? 满足:
是非空的有限几何,? 是 A 中某些指定的非空子集组成的子集族,称 ? 满足:
1、单点集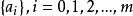 都属于 ? 。
都属于 ? 。
2、对于 A 的每一个指定子集的非空子集还是一个指定子集,即,如果 S,S’ 是 A 的子集,并且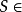 ?,
?,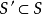 ,那么
,那么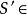 ?。
?。
定义设 ? 是抽象复形,若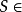 ?,则称 S 为抽象单形;当 S 中有 q+1 个元素时,称 S 为 q 维抽象单形;零维抽象单形称为顶点;? 中诸抽象单形的维数最大值,称为抽象复形 ? 的维数。1
?,则称 S 为抽象单形;当 S 中有 q+1 个元素时,称 S 为 q 维抽象单形;零维抽象单形称为顶点;? 中诸抽象单形的维数最大值,称为抽象复形 ? 的维数。1
性质如果一个抽象单形S作为A的子集所含元素个数为n+1,则S称为n维单形。抽单形S和S'作为A 的子集有包含关系S'⊂S.则称S'是S的一个面。
如果一个抽象复形?与一个单纯复合形K的顶点之间建立了一个一一对应,并且在此对应下,K的一个顶点的子集是K中某一单纯形的顶点集当且仅当其对应像是?中某一抽象单形的顶点集,那么单纯复合形K称为抽象复形?的几何实现。一个抽象单形总是有几何实现的,但不唯一,同一抽象单形的不同几何实现有着相同的单纯形之间的包含与相交关系。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国