实数公理是定义实数的一种途径。按照它,所谓实数系就是定义了两种二元运算(加法与乘法)和一种次序关系(>)的集合,并且这些运算和次序满足规定的公理,由这些公理可以推出实数的一切性质。
简介实数公理是定义实数的一种途径。按照它,所谓实数系就是定义了两种二元运算(加法与乘法)和一种次序关系(>)的集合,并且这些运算和次序满足规定的公理,由这些公理可以推出实数的一切性质。
具体内容实数公理的具体内容如下:
设R是一个集合,若它满足下列三组公理,则称为实数系,它的元素称为实数:
(I)域公理
对任意 a,b∈R ,有 R 中惟一的元素 a+b 与惟一的元素 a·b 分别与之对应,依次称为 a , b 的和与积,满足:
1.(交换律) 对任意 a,b∈R ,有a+b=b+a,a·b=b·a 。
2.(结合律) 对任意 a,b,c∈R ,有a+(b+c)=(a+b)+c,a·(b·c)=(a·b)·c 。
3.(分配律) 对任意a,b,c∈R,有(a+b)·c=a·c+b·c 。
4.(单位元) 存在R中两个不同的元素,记为0,1分别称为加法单位元与乘法单位元,使对所有的a∈R,有a+0=a,a·1=a 。
5.(逆元) 对每个 a∈R ,存在 R 中惟一的元素,记为 -a ,称为加法逆元;对每个 a∈R\{0} ,存在 R 中惟一的元素,记为 a-1 ,称为乘法****逆元,使a+(-a)=0,a·a-1=1 。
(II) 序公理
**(a)**在任意两个元素 a,b∈R 之间存在一种关系,记为“>”,使对任意 a,b,c∈R ,满足:
1.(三歧性)a>b,b>a,a=b 三种关系中必有一个且仅有一个成立。
2.(传递性) 若 a>b 且 b>c 则 a>c 。
3.(与运算的相容性) 若 a>b,则 a+c>b+c;若 a>b,c>0 则 ac>bc 。
**(b)**在任意两个元素 a,b∈R 之间存在一种关系,记为“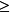 ”,使对任意 a,b,c∈R ,满足:
”,使对任意 a,b,c∈R ,满足:
1.(反对称性) 若 a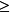 b 且 b
b 且 b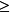 a 那么 a=b 。
a 那么 a=b 。
2.(传递性) 若 a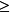 b 且 b
b 且 b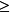 c 则 a
c 则 a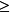 c 。
c 。
3.(与运算的相容性)若 a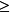 b,则 a+c
b,则 a+c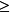 b+c ;若 a
b+c ;若 a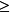 0 且 b
0 且 b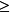 0,则 ab
0,则 ab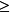 0 。
0 。
注:对于序公理a,b这两种描述是等价的。因为我们可以通过其中一个符号及其性质来定义另一个符号。
(III)(1) 阿基米德公理(也称阿基米德性质,它并不是严格意义上的公理,可以由连续性公理证明。在欧几里得的几何书中,它仅被描述为一个命题)。
阿基米德公理:对任意a,b∈R,a>0 存在正整数 n ,使 na>b 。
****(III)(2)完备性公理
R中的任何基本列都在R中收敛。
称满足公理组I的集为域;满足公理组I与II的集为有序域;满足公理组I,II**与(III)(1)的集为阿基米德有序域;满足公理组I~III的集为完备阿基米德有序域或完备有序域**。这样,实数系就是完备阿基米德有序域。所有有理数的集合Q就是阿基米德有序域,但它不满足完备性公理。根据域公理,可以定义实数的减法和除法,并证明四则运算的所有性质。序公理的1与2表明关系“>”是R的全序。
用域公理和序公理可以定义正数、负数、不等式、绝对值,并证明它们具有通常的运算性质。加上阿基米德公理与完备性公理,可以证明实数的其他性质以及幂、方根、对数等的存在性。实数公理有多种不同的提法,常见的另一种提法是把公理组III****换成
****(III)’连续性公理(戴德金公理)
若 A,B 是 R 的非空子集且 A∪B=R ,又对任意的 x∈A 及任意的 y∈B 恒有 x




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国