[科普中国]-磁隧道结效应-

在 MTJs中，TMR效应的产生机理是自旋相关的隧穿效应。MTJs的一般结构为铁磁层 /非磁绝缘层 /铁磁层(FM/I/FM) 的三明治结构。饱和磁化时，两铁磁层的磁化方向互相平行，而通常两铁磁层的矫顽力不同，因此反向磁化时，矫顽力小的铁磁层磁化矢量首先翻转，使得两铁磁层的磁化方向变成反平行。电子从一个磁性层隧穿到另一个磁性层的隧穿几率与两磁性层的磁化方向有关。

量子隧道效应量子隧道效应是基本的量子现象之一，即当微观粒子的总能量小于势垒高度时，该粒子仍能穿越这一势垒。如图，纵坐标为能量的多少。按经典理论，粒子为脱离此能量的势垒，必须从势垒的顶部越过。但由于量子力学中的量子不确定性，时间和能量为一组共轭量。在很短的时间中（即时间很确定），能量可以很不确定，从而使一个粒子看起来像是从“隧道”中穿过了势垒。在诸如能级的切换，两个粒子相撞或分离的过程（如在太阳中发生的仅约1000万摄氏度的“短核聚变”）中，量子隧道效应经常发生。

发展历史早在1975年,Julliere就在Co/Ge/Fe磁性隧道结(MagneticTunnelJunctions，MTJs)（注：MTJs的一般结构为铁磁层/非磁绝缘层/铁磁层(FM/I/FM)的三明治结构）中观察到了TMR效应。但是，这一发现当时并没有引起人们的重视。在这之后的十几年内，TMR效应的研究进展十分缓慢（注：TMR效应产生机理是自旋相关的隧穿效应。）

1988年,巴西学者Baibich在法国巴黎大学物理系Fert教授领导的科研组中工作时，首先在Fe/Cr多层膜中发现了巨磁电阻(GMR)效应。TMR效应和GMR效应的发现导致了凝聚态物理学中新的学科分支——磁电子学的产生。20年来，GMR效应的研究发展非常迅速，并且基础研究和应用研究几乎齐头并进，已成为基础研究快速转化为商业应用的国际典范1。

随着GMR效应研究的深入，TMR效应开始引起人们的重视。尽管金属多层膜可以产生很高的GMR值，但强的反铁磁耦合效应导致饱和场很高，磁场灵敏度很小，从而限制了GMR效应的实际应用。MTJs中两铁磁层间不存在或基本不存在层间耦合，只需要一个很小的外磁场即可将其中一个铁磁层的磁化方向反向，从而实现隧穿电阻的巨大变化，故MTJs较金属多层膜具有高得多的磁场灵敏度。同时，MTJs这种结构本身电阻率很高、能耗小、性能稳定。因此，MTJs无论是作为读出磁头、各类传感器，还是作为磁随机存储器(MRAM)，都具有无与伦比的优点，其应用前景十分看好，引起世界各研究小组的高度重视。

效应在两块铁磁薄片之间夹一层厚度约为0.1nm的极薄绝缘层，构成所谓的结元件。

在铁磁材料中，由于量子力学交换作用，铁磁金属的 3d轨道局域电子能带发生劈裂，使费米(Fermi)面附近自旋向上和向下的电子具有不同的能态密度。

若两层磁化方向互相平行，则在一个磁性层中，多数自旋子带的电子将进入另一磁性层中多数自旋子带的空态，少数自旋子带的电子也将进入另一磁性层中少数自旋子带的空态，总的隧穿电流较大；若两磁性层的磁化方向反平行，情况则刚好相反，即在一个磁性层中，多数自旋子带的电子将进入另一磁性层中少数自旋子带的空态,而少数自旋子带的电子也将进入另一磁性层中多数自旋子带的空态,这种状态的隧穿电流比较小。

因此,隧穿电导随着两铁磁层磁化方向的改变而变化，磁化矢量平行时的电导高于反平行时的电导。

公式MTJs中两铁磁层电极的自旋极化率定义为：

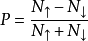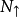其中，和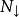分别为铁磁金属费米面处自旋向上和自旋向下电子的态密度。

隧道磁阻TMR：

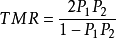
式中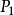和分别为两金属层的自旋极化率。

展望由于MTJs中两铁磁层间不存在或基本不存在层间耦合，只需要一个很小的外磁场即可将其中一个铁磁层的磁化方向反向，从而实现隧穿电阻的巨大变化，故MTJs较金属多层膜具有高得多的磁场灵敏度同时， MTJs这种结构本身电阻率很高、能耗小、性能稳定，因此，MTJs无论是作为读出磁头、各类传感器，还是作为磁随机存储器MRAM），都具有无与伦比的优点。

但就用于计算机读磁头来说，要想使MTJs型的TMR读磁头在读取速率和噪声两方面均优于当前的自旋阀型GMR读磁头， MTJs的RA值则应低于4Ωμm。目前所能获得的最佳PSV型MTJs的RA值比这一数值仍然高出2个数量级。

研究与开发室温TMR值高、热稳定性好、RA值低、成本低的TMR材料将是今后磁电阻材料领域工作的重点和关键，其中低RA值的PSV型MTJs材料的研究和开发有望成为实现这一目标的突破口

本词条内容贡献者为:

张磊 - 副教授 - 西南大学