[科普中国]-伴侣矩阵

伴侣矩阵亦称友矩阵，是矩阵标准形理论中一类重要的矩阵。

简介伴侣矩阵亦称友矩阵，矩阵标准形理论中一类重要的矩阵。

设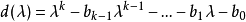 是数域 P 上的首一多项式，则 P 上的矩阵

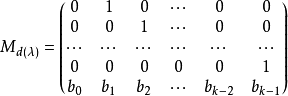称为多项式 d(λ) 的伴侣矩阵。设 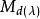是 d(λ) 的友矩阵，则特征矩阵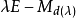的不变因子是1,1,...,d(λ)。1

相关定理定理1每一个首 1 多项式既是它的友矩阵的最小多项式，又是它的友矩阵的特征多项式。

如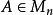的极小多项式的次数为 n ，那么与每一个特征值对应的最大的Jordan块就是与每一个特征值对应的唯一的Jordan块．这样的矩阵是无损的，特别地，每一个友矩阵都是无损的，当然，不一定每个无损的矩阵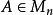都是友矩阵，但是 A 与 A 的特征多项式的友矩阵 C 有同样的Jordan标准型(与每一个不同的特征值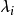对应的只有一个分块，所以 A 与 C 相似。

定理2设 C 为多项式 p(x) 的友矩阵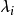，是 C 的特征值，则

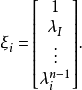是 C 的对应于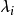的特征向量。

定理3n 阶复数矩阵 A 相似于它的特征多项式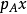的友钜阵，当日仅当 A 的最小多项式与特征多项式相同。

定理4设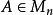有极小多项式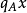以及特征多项式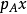，则下面诸结论等价：

(a)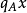的次数为n；

(b)=；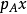

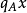(c)A是无损的；

(d)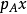与P^(t)的友矩阵相似。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学