[科普中国]-阿波罗尼奥斯轨迹定理

阿波罗尼奥斯轨迹定理是一个著名轨迹问题。若一动点至两定点的距离之比等于两不等的已知线段之比，则该点的轨迹是一个圆。

简介阿波罗尼奥斯轨迹定理是一个著名轨迹问题。

若一动点至两定点的距离之比等于两不等的已知线段之比，则该点的轨迹是一个圆。如果 A，B 为定点，P 是动点，a，b 为不等的已知线段，PA/PB=a/b，Q，R 为线段 AB 的内、外分点，即 QA/QB=RA/RB=a/b，则点的轨迹是以 QR 为直径的圆（如图）。

这个圆称为阿波罗尼奥斯圆。1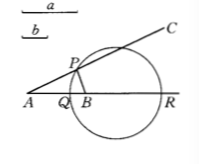

阿波罗尼奥斯问题阿波罗尼奥斯问题是由公元前 3 世纪下半叶古希腊数学家阿波罗尼奥斯提出的几何作图问题，载于他的《论接触》中，惜原书已失传。后来公元 4 世纪学者帕波斯记载了其中所提出的一个作图问题：设有 3 个图形，可以是点、直线或圆，求作一圆通过所给的点（如果3个图形中包含点的话）并与所给直线或圆相切。当中共有 10 种可能情形，其中最著名的是：求作一圆与3个已知圆相切，常称为阿波罗尼奥斯问题（ Apollonius'problem）。据说阿波罗尼奥斯本人解决了问题，可惜结果没有流传下来。

1600年法国数学家韦达在一篇论着中应用了两个圆相似中心的欧几里得解法，通过对每一种特殊情况的讨论，严格陈述了该问题的解。后来牛顿、蒙日、高斯等许多数学家都对这一问题进行过研究，得到多种解决方法。 其中以法国数学家热尔岗约于1813年给出的解法较有代表性。以上所说都是通常的标尺作图法。如果放宽作图条件限制，则有多种简捷的解法。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学