贝特朗假设是关于素数分布的一个著名结论。对任一实数 x≥1,在 x 及 2x 之间必有一素数。此假设是贝特朗 (Bertrand,J.L.F.)于 1846 年为证明置换群理论中的一个定理而作出。
简介贝特朗假设是关于素数分布的一个著名结论。
对任一实数 x≥1,在 x 及 2x 之间必有一素数。此假设是贝特朗 (Bertrand,J.L.F.)于 1846 年为证明置换群理论中的一个定理而作出。
证明贝特朗假设于1848 年即被切比雪夫 (Чебышeв,П.Л) 所证明,他引入函数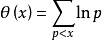 和
和
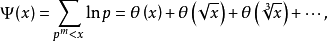
并证明
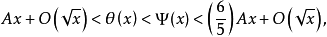 其中
其中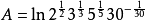 ,此猜测被证明后即称为贝特朗定理。
,此猜测被证明后即称为贝特朗定理。
难题关于 x 及 2x 之间的素数问题,目前已经证明比贝特朗定理要好得多的结果:存在一个小于 1/2 的正常数 c,在 x 于 x+xc 之间必有素数存在,对于这样的 c,是否存在一个正的下界,是目前正在研究的难题之一。1
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国