[科普中国]-半正定二次型

定型二次型是实二次型的类型。正定、半正定、负定、半负定的二次型合称为定型二次型；不定的二次型称为不定型二次型。

简介引入定型二次型是实二次型的类型。

设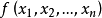 是一个实二次型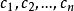， 是任意 n 个不全为零的实数。实二次型分类如下：

1、若恒有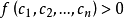，则 f 称为正定的。

2、若恒有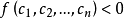，则 f 称为负定的。

3、若恒有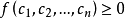，则 f 称为半正定的。

4、若恒有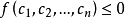，则 f 称为半负定的。

5、其他情形的 f 称为不定的。

定义正定、半正定、负定、半负定的二次型合称为定型二次型；不定的二次型称为不定型二次型。

高斯 (Gauss,C.F.) 在 1801 年出版的《算术的研究》中包含了对二次型的探讨。他用行列式表示二次型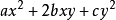 的判别式，还引进了正定、半正定、负定的概念。他引进的负定概念实际上是现在的半负定。1

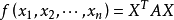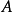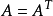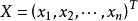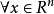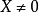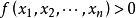正定二次型设，其中矩阵是对称阵，即，为列向量，若，，有，则称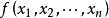为正定二次型，称实对称矩阵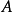正定。

例如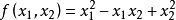，即为正定二次型，其中，。

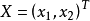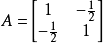本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学