[科普中国]-包含公理

并集公理可以得出包含公理：对任意两集 X 与 Y，存在同时以 X，Y 为子集的集合。

简介引入并集公理(axiom of inclusion)是集合论的一条重要公理。由策梅洛 (Zermelo,E.F.F.) 于 1908 年提出。该公理断言：对任何集合 X，存在 X 的所有元素的并集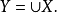 这条公理可以形式化为：

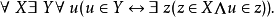利用这条公理可以定义集合的并运算。

例如， 等。也可以定义集合的包含关系：

定义由于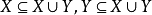 ，所以，从并集公理可以得出包含公理：对任意两集 X 与 Y，存在同时以 X，Y 为子集的集合。1

策梅洛-弗兰克尔集合论策梅洛-弗兰克尔集合论的公理由一阶逻辑的逻辑公理和八条非逻辑公理组成。

(1)同一律（外延公理）：两个集合相等的充分必要条件是它们具有相同的元素，即

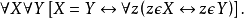
(2)配对集公理：任给两个集合X和Y，都有一个恰好由它们组成的集合{X,Y}，即

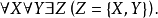
(3)并集公理：任给一个集合X，都有一个恰好由X的元素的元素之全体所组成的集合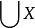 ，即

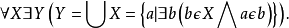
(4)幂集公理：任给一个集合X，都有一个恰好由它的子集合的全体组成的集合P(X)，即

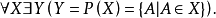
(5)无限集公理：存在一个满足如下两条要求（a）和（b）的集合X，

（a）X含一个元素；

（b）如果Y∈X，那么Y∪{Y}∈X。其中Y∪{Y}={Y,{Y}}，即

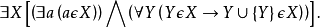
(6)分解原理：分解公理又称概括公理，应当注意到这里的表达式并非朴素集合论的概括方式。设φ(x,y₁,…，y𝗇)（1≤n