[科普中国]-凹筝形

筝形 (kite) 亦称偏菱形。筝形分凸筝形和凹筝形两种。特殊的四边形之一。凹筝形又称鸢形。

简介筝形 (kite) 亦称偏菱形。特殊的四边形之一。有一条对角线是另一条对角线的垂直平方线的四边形称为筝形。筝形分凸筝形和凹筝形两种。

凹筝形又称鸢形。筝形是轴对称图形，其中一条对角线为对称轴。如图中，对角线 AC 分别为它们的对称轴。凸筝形有一个内切圆，凹筝形有一个旁切圆。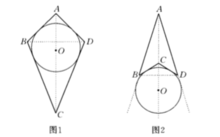

判定①两组邻边分别相等的四边形是筝形。

②有一条对角线垂直平分另一条对角线的四边形是筝形。

显然，菱形是特殊的筝形。

性质1.轴对称。对称轴为筝形不相等的一对角的对角线所在直线。

2.有一组对角相等。为方便讨论，不妨把这组对角称为“等角”

3.有两组邻边分别相等。

4.一条对角线所在的直线垂直平分另一条对角线

5.筝形的面积公式：

①S=mn/2，其中m、n是两条对角线长。

②S=absinA，其中a、b是筝形的一组对边，A是筝形的等角。

③S=(a2sinB+b2sinC)/2，其中B、C为筝形不相等的一组对角。

6.筝形的周长公式：C=2(a+b)。

7.筝形有内切圆，内切圆圆心是筝形的对称轴和等角的平分线的交点。

8.筝形有外接圆的充要条件为：2ab=mn或A=90度或B+C=180度

9.筝形的内切圆和四条边的四个切点的连线是等腰梯形，筝形的内切圆和两条对角线的4个交点的连线仍为筝形。1

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学