[科普中国]-场强张量

电磁张量（electromagnetic tensor）或电磁场张量（electromagnetic field tensor）（有时也称作场强张量（field strength tensor）、法拉第张量（Faraday tensor）或麦克斯韦双矢量（Maxwell bivector））是一个描述一物理系统中电磁场的数学客体，所根据的是麦克斯韦的电磁学理论。场张量是在赫尔曼·闵可夫斯基提出狭义相对论的四维张量形式之后被首次使用。

细节电磁张量 常表示成如下矩阵形式：

其中E是电场，B是磁场，c是光速。

性质从场张量的矩阵形式可以见到，其须满足下列特性：

反对称性： （因此称作双矢量（或称双矢、二重矢量，bivector））。

零值的迹数或称对角和。

6个独立分量——

若将场张量做内积，则可得到一洛伦兹不变量：

场张量 与对偶张量的乘积则为一伪标量不变量（pseudoscalar invariant）：

其中 为四阶完全反对称单位张量（completely antisymmetric unit tensor）或称列维-奇维塔符号（Levi-Civita symbol）。注意到场张量的行列式

更正式地，可将电磁张量以4-矢势 写成：

其中4-矢势为： ，其协变（covariant）形式可以透过乘上闵可夫斯基度规 来得到：

此处闵可夫斯基度规 的定义为：

若按照另种使用习惯将闵可夫斯基度规定义为：

则4-矢势的协变形式会是：

导出电磁张量为了要导出电磁张量的所有矩阵元素，我们需要定义（时空）导数算符（derivative operator）：

以及4-矢势：

其中 为矢势，而 为其分量， 为标势， 为光速；指标α取值0、1、2、3。

电场与磁场可以透过下面两个与矢势及标势的关系式导出：

以x分量为例：

利用这样的定义，我们可以将上面两个式子改写成： ，或将c移动到等号左边：

在评估过所有分量后，可以得到一个二阶、反对称、协变张量 ：

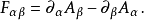
在量子电动力学与量子场论中的角色在量子电动力学中的拉格朗日量是从相对论建立的经典拉格朗日量所延伸：以将光子以及电子的创生（creation）与湮灭（annihilation）整合进来。

在量子场论中，电磁场强度张量被当作是规范场强度张量的范本。此一项搭配上局域相互作用拉格朗日量（local interaction Lagrangian），其作用角色与在量子电动力学中几乎一样。2

相关条目麦克斯韦方程组

电磁学

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学