[科普中国]-导热微分方程

导热微分方程是对导热物体内部温度场内在规律的描述，适用于所有导热过程。

导热微分方程和傅里叶定律傅里叶定律是在实验的基础上建立起来的，它指出，导热热流密度的大小与温度梯度的绝对值成正比，其方向与温度梯度的方向相反

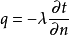（1-1）

因为热量传递方向与温度梯度的方向相反，所以等式中有一负号，傅里叶定律的本质是说，在有温度差的物系内部，热流总是朝着温度降低的方向。

当给定导热面上热流密度相等时

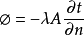（1-2）

傅里叶定律揭示了连续温度场内热流密度与温度梯度的关系。对于一维稳态导热问题可直接利用傅里叶定律积分求解，求出导热热流量。但由于傅里叶定律未能揭示各点温度与其相邻点温度之间的关系，以及此刻温度与下一时刻温度的联系，对于多维稳态导热和一维及多维非稳态导热问题都不能直接利用傅里叶定律积分求解。导热微分方程揭示了连续物体内的温度分布与空间坐标和时间的内在联系，使上述导热问题求解成为可能。

根据傅里叶定律和能量守恒方程，可以推得直角坐标下的导热微分方程

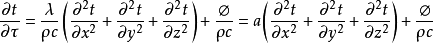（1-3）

式中，a为热扩散率，又称导温系数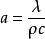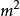，，/s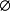；为单位时间内、单位体积中内热源生成的热量，W/。

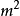导热微分方程是对导热物体内部温度场内在规律的描述，适用于所有导热过程，要获得特定情况下导热问题的解，必须附加该情况下的限制条件，这些条件称为定解条件。定解条件包括时间条件和边界条件。所以，导热问题完整的数学描述包括导热微分方程和相应的定解条件。时间条件给定某一时刻导热物体内的温度分布，称为初始条件。稳态导热时，导热物体内的温度分布不随时间变化，初始条件没有意义，所以非稳态导热才有初始条件。边界条件是指导热物体边界处的温度或表面传热情况。边界条件通常分为三类：

（1）第一类边界条件：给定物体边界上任何时刻的温度分布。

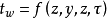（1-4）

（2）第二类边界条件：给定物体边界上的热流密度分布。

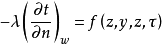（1-5）

（3）第三类边界条件：给定物体边界与周围流体间的表面传热系数h及流体的温度。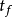

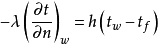（1-6）

以上三类边界条件之间有一定的联系。当物体边界温度等于流体温度，第三类边界条件变成第一类边界条件。边界面的便面传热系数h为零，第三类边界条件变成特殊的第二类边界条件——物体边界面绝热。1

导热系数导热系数是物质的一个物性参数，表示物质导热能力的大小。由式（1-1）得

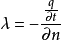
即导热系数的数值等于温度梯度为1K/m时，单位时间内通过单位面积的导热量。不同物质的导热系数彼此不同，即使是同一物质，导热系数的值也随压力、温度以及该物质内部结构、温度等因素而变化。物质的导热系数通常由实验确定。

各种物质导热系数的范围为：气体0.006~0.6W/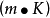；液体0.07~0.7W/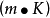；金属6~470W/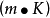；保温与建筑材料0.02~3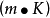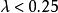W/。W/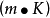的材料，常称作绝热保温材料，如石棉、膨胀珍珠岩、玻璃纤维制品等。

金属材料的导热系数比非金属材料高，纯金属的导热系数又比合金高，各种纯金属中以银的导热系数为最高。通常，气体的导热系数为最小，而且在较大的压力范围内，气体的导热系数只是温度的函数，与压力无关。除液态金属，液体材料中的水的导热系数是最大的。

各种材料的导热系数随温度变化的规律不尽相同。纯金属的导热系数一般只随温度升高而下降。气体的导热系数随温度的升高而增大。除水和甘油外，一般液体的导热系数一般随温度的升高而减小。保温与建筑材料的导热系数大多数随温度升高而增大，还与材料的结构、孔隙度、密度和湿度有关。

在一定温度范围内，大多数工程材料的导热系数可以近似认为是温度的线性函数，即

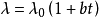
式中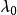，为0℃时按上式计算的导热系数（一般，它并非0℃时的实际值）；b为由实验确定的常数。1

初始条件和边界条件热传导方程式中有对时间的一阶偏导，因此，在求非稳态导热时要有初始条件，常用的初始条件为：

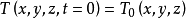（在V内） （1-7）

式中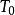，——t=0时的温度分布状态；

V——体域。

传热问题中常见的几种边界条件如下：

（1）给出温度值的边界：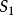

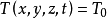（对于t>0，在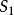上） （1-8）

（2）给出热通量Q的边界：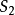

（在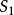上） （1-9）

式中，——边界外法向的方向余弦。

（3）给出热损失的边界：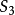

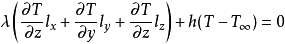（在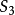上） （1-10）

式中，h——放热系数；

——环境温度。 2

本词条内容贡献者为:

陈红 - 副教授 - 西南大学