[科普中国]-叠式存储算法

叠式存储算法(stack algorithm)又称堆栈算法，叠式存储算法的思想很简单，它的序列译码的基本概念明显易懂。译码器由一种编排好的表格或称堆栈组成。在堆栈内，把已探寻过的路径，按其对数似然值的降序排列好。堆栈顶端存储着该堆栈全部存储路径中最大对数似然函数的路径。由于该路径与正确路径最相似，所以，它是下一步被研究的对象(每深入一级，延伸出两条支路)。随着每次延伸之后，堆栈就重新排列一次。其结果是，哪一条路径的对数似然函数增大，那它就是下一步被继续研究的对象。如果该路径的对数似然函数减小，那么，它就要从顶端位置落下，并储存在堆栈适当的位置上，从而得到一个新的顶端节点。把每一条已探明的路径用其最终的节点来表示，则堆栈便可等效地看成是一张节点目录表，而节点则是按其对数似然函数值排列的。这样，译码器的目的就是寻求顶端节点，再延伸其后继节点，然后对堆栈作适当重新排列。当把起始原节点装入堆栈后，此节点的对数似然函数就取为零。译码算法包括下列步骤：1．计算其顶端节点的全部后继节点的对数似然函数，并在堆栈适当的位置上把新的路径存进去。2．当节点的后继节点一旦被存入堆栈后，该节点便在堆栈上被消除。3．如果新的顶端节点是最后节点，则运算停止或转回到第1级上去。当运算从回路系统中逸出时，顶端节点就是译码所得路径的端节点。于是，整个译码路径就很容易从堆栈所存储的信息中求得1。

基本介绍叠式存储译码(或称堆栈存储译码)法是序列译码方法的一种，是扎岗基洛夫和杰里涅克于1966年和1969年分别独立地发现这种算法，简称ZJ算法。这种算法依然是根据费诺度量，译码器在码树上寻找正确路径时，力求尽早地排除所有的非最大似然路径，从而使译码器的平均计算量减少。

在叠式译码算法中，有一个大容量的存储器，或称之为叠式****存储器(以下简称：SS)，用来存储被比较的不同长度的路径及其路径值。在译码过程中的每一步(每比较、计算一次)，把具有最大路径值的路径及其度量值存入SS最上一行(第一行)，其它的以度量值递减的次序，将其路径和度量依次存放在SS中。当译码进行到下一步时，译码器计算存放在SS中第一行路径的后续2k0个分支的度量值，并与存储在第一行的度量值相加，从而得到2k0个新的度量值，并且把这些新的度量值与SS中其它行的度量值进行比较，根据比较结果，按照度量值的大小重新排列，把具有最大度量值的路径及其量值放在SS中第一行，取代了原来存放在第一行的内容，其余的按度量值递减的次序捧列。当译码进行到某一步后，若SS中第一行的路径已达到码树的终端节点(第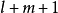 阶节点)，则译码完毕，译码器输出SS中的第一行路径作为判决路径输出。因此，叠式译码算法所判决的路径是具有最大似然函数的路径2。

算法步骤叠式存储算法包括下列步骤：

1．从码树的起始节点(第0阶节点)开始译码，SS中全部为零。

2．计算存在SS第一行的路径后续各分支的度量值，并与原来存储的度量值相加。

3．删去SS第一行原存储的内容。

4．挑选一条有最大度量值的路径存入SS的第一行。若有一条以上的路径具有最大度量值，则任选一条，并且按度量值递减的次序，重新排列SS中的次序和内容。

5．若SS中第一行的路径已处在码树的终点，则中止译码。否则回到第二步。

6．译码完毕后，译码器把第一行的内容输出给用户2。

叠式存储算法的特点叠式存储算法有如下特点：

1．与费诺算法相同，译码器译每一帧(L段)接收序列的计算次数，随信道干扰的大小而变化，若干扰严重，错误个数增加，则计算次数加大，反之则减少，平均计算次数也与m无关，因此可以选用大m也就是自由距离大的码，从而使误码率做的很小。

2．需要大容量的存储器。因为每译一步，就要有(2k0－1)组数据存入到SS存储器。

3．也必须有一个输入缓存器，存储输入给译码器的接收序列，以便在译码过程中从一个节点跳向另一个节点时，使用以前的码段，以及存储此时刻后的接收码段。如费诺算法一样，在干扰严重情况下，译码器搜索时间很长，也可能引起译码器溢出。一般，当发生溢出时，应向用户发出告警信号，表示这一帧信号有误，或者，在有反馈信道情况下，经反馈信道要求发端重发。

4．有比费诺算法较高的译码速度，但需要SS存储器。由于费诺算法不需要SS存储器，而且也能达到比较高的译码速度，所以在实用中，费诺算法要比叠式存储算法应用的广泛2。

本词条内容贡献者为:

李岳阳 - 副教授 - 江南大学