[科普中国]-薛定谔绘景

薛定谔绘景（Schrödinger picture）是量子力学的一种表述，为纪念物理学者埃尔温·薛定谔而命名。在薛定谔绘景里，量子系统的态矢量随着时间流易而演化，而像位置、自旋一类的对应于可观察量的算符则与时间无关。

薛定谔绘景与海森堡绘景、狄拉克绘景不同。在海森堡绘景里，对应于可观察量的算符会随着时间流易而演化，而描述量子系统的态矢量则与时间无关。在狄拉克绘景里，态矢量与算符都会随着时间流易而演化。

这三种绘景殊途同归，所获得的结果完全一致。这是必然的，因为它们都是在表达同样的物理现象。

简介薛定谔绘景（Schrödinger picture）是量子力学的一种表述，为纪念物理学者埃尔温·薛定谔而命名。在薛定谔绘景里，量子系统的态矢量随着时间流易而演化，而像位置、自旋一类的对应于可观察量的算符则与时间无关。

薛定谔绘景与海森堡绘景、狄拉克绘景不同。在海森堡绘景里，对应于可观察量的算符会随着时间流易而演化，而描述量子系统的态矢量则与时间无关。在狄拉克绘景里，态矢量与算符都会随着时间流易而演化。

这三种绘景殊途同归，所获得的结果完全一致。这是必然的，因为它们都是在表达同样的物理现象。

在薛定谔绘景里，负责时间演化的算符是一种幺正算符，称为时间演化算符。假设时间从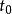 流易到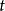 ，而经过这段时间间隔，态矢量 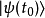演化为态矢量 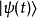，这时间演化过程以方程表示为

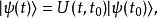其中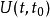， 是时间演化算符。

假设系统的哈密顿量H不含时，则时间演化算符为

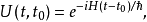其中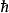， 是约化普朗克常数，指数函数 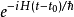必须通过其泰勒级数计算。

在初级量子力学教科书里，时常会使用薛定谔绘景。1

时间演化算符定义时间演化算符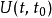 定义为

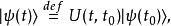其中，右矢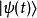 表示时间为t的态矢量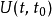， 是时间演化算符，从时间t演化到时间 。

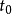这方程可以做这样解释：将时间演化算符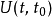 作用于时间是 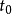的态矢量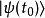 ，则会得到时间是t的态矢量 。

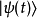类似地，也可以用左矢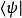 来定义：

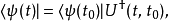其中，算符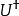 是算符U的厄米共轭。

性质幺正性

由于态矢量必须满足归一条件，态矢量的范数不能随时间而变：

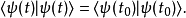可是，

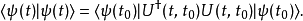所以，时间演化算符必须是幺正算符。

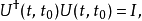其中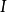， 是单位算符。

单位性

时间演化算符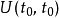 必须是单位算符 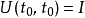，因为，

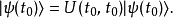
闭包性

从初始时间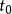 到最后时间t的时间演化算符，可以视为从中途时间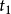到最后时间t的时间演化算符，乘以从初始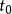时间到中途时间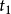的时间演化算符：

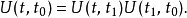
根据时间演化算符的定义，

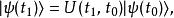
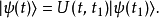所以

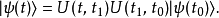可是，再根据定义

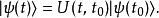所以，时间演化算符必须满足闭包性：

时间演化算符的微分方程为了方便起见，设定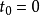，初始时间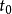永远是0，则可忽略时间演化算符的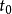参数，改写为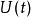。含时薛定谔方程为

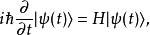其中，H是哈密顿量。

从时间演化算符的定义式，可以得到

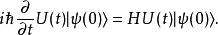
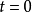由于可以是任意恒定态矢量（处于的态矢量），时间演化算符必须遵守方程

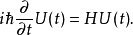
假若哈密顿量不含时，则这方程的解答为

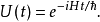注意到在时间t=0，时间演化算符必须约化为单位算符U(0)=I。由H是算符，指数函数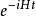必须通过其泰勒级数计算：

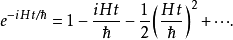
按照时间演化算符的定义，在时间t，态矢量为

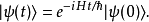注意到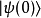可以是任意态矢量。假设初始态矢量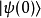是哈密顿量的本征态，而本征值是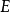，则在时间t，态矢量为

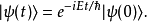这样，可以看到哈密顿量的本征态是定态，随着时间的流易，只有相位因子在进行演化。

假设，哈密顿量与时间有关，但在不同时间的哈密顿量相互对易，则时间演化算符可以写为

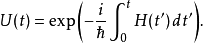假设，哈密顿量与时间有关，而在不同时间的哈密顿量不相互对易，则时间演化算符可以写为

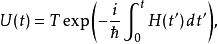其中，T是时间排序算符。

必须用戴森级数来表示，

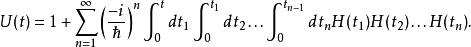
参阅哈密顿-亚可比方程

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学