[科普中国]-哈密顿-雅可比-爱因斯坦方程

在广义相对论中，哈密顿-雅可比-爱因斯坦方程（英语：Hamilton–Jacobi–Einstein equation，简称HJEE）是一道哈密顿形式、描述超空间中的几何力学的方程。创于“几何力学年代”，这方程由亚瑟·佩雷斯（Asher Peres）在1960给出，目的是更正广义相对论以令其成为量子理论的半古典近似，就像量子力学与古典力学一样对应关系。

简介在广义相对论中，哈密顿-雅可比-爱因斯坦方程（英语：Hamilton–Jacobi–Einstein equation，简称HJEE）是一道哈密顿形式、描述超空间中的几何力学的方程。创于“几何力学年代”，这方程由亚瑟·佩雷斯（Asher Peres）在1960给出，目的是更正广义相对论以令其成为量子理论的半古典近似，就像量子力学与古典力学一样对应关系。

这方程包含了全部10道爱因斯坦场方程式（EFEs），亦是古典力学中哈密顿-雅可比方程式（HJE）的修正，并可以从ADM形式中的爱因斯坦-希尔伯特作用量，以最小作用量原理推导。1

背景及动机古典与量子物理的对应关系古典分析力学中的一个系统的动力学是由作用量S所概括。而各量子理论，即非相对论量子力学、相论对量子力学及量子场论，各有不同的诠释及数学形式，但一个系统的行为都是完全由一个复机率幅Ψ（正式来说是量子态的ket|Ψ⟩－希尔伯特空间中的元素)。Eikonal的半古典近似给出

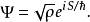
当中Ψ的相位可被诠释为作用量，而模值√ρ=√Ψ*Ψ= |Ψ|则可被根据哥本哈根诠释为机率密度函数。约化普朗克常数ħ是“作用量的量子”。代入一般形式的薛定谔方程式（SE），则有

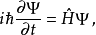取ħ→ 0极限则得到古典的HJE：

这是对应原理其中一个结果。1

哈密顿力学哈密顿力学是哈密顿于1833年建立的经典力学的重新表述，它由拉格朗日力学演变而来。拉格朗日力学是经典力学的另一表述，由拉格朗日于1788年建立。哈密顿力学与拉格朗日力学不同的是前者可以使用辛空间而不依赖于拉格朗日力学表述。关于这点请参看其数学表述。

适合用哈密顿力学表述的动力系统称为哈密顿系统。2

爱因斯坦场方程爱因斯坦重力场方程是一组含有十个方程的方程组，由爱因斯坦于1915年在广义相对论中提出。此方程组描述了重力是由物质与能量所产生的时空弯曲所造成。也就是说，如同牛顿的万有引力理论中质量作为重力的来源，亦即有质量就可以产生重力，爱氏的相对论理论更进一步的指出，动量与能量皆可做为重力的来源，并且将“重力场”诠释成“时空弯曲”。所以当我们知道物质与能量在时空中是如何分布的，就可以计算出时空的曲率，而时空弯曲的结果即是重力。

爱因斯坦重力场方程是用来计算动量与能量所造成的时空曲率，再搭配测地线方程，就可以求出物体在重力场中的运动轨迹。这个想法与电磁学的想法是类似的：当我们知道了空间中的电荷与电流(电磁场的来源)是如何分布的，借由麦克斯韦方程组，我们可以计算出电场与磁场，再借由劳伦兹力方程，即可求出带电粒子在电磁场中的轨迹。

仅在一些简化的假设下，例如：假设时空是球对称，此方程组才具有精确解。这些精确解常常被用来模拟许多宇宙中的重力现象，像是黑洞、膨胀宇宙、引力波。3

参阅物理学主题

哈密顿原理

经典力学

拉格朗日力学

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学